Prime numbers: what are they and how to find them?

we call Prime number a natural number what has two dividers: 1 and himself. To find prime numbers, the sieve of Eratosthenes was developed. When a number is not prime, we can write it as the multiplication of prime numbers, a process called factorization.

Read too: What is the value of a digit?

How do you know if a number is prime?

Searching for prime numbers is quite common in Mathematics. When we divide one number by another and the result is exact, that is, it leaves no rest, this number is called a divisor. To identify whether a number is prime or not, we need to know what the divisors of that number are. If this number has exactly two dividers: 1 and himself, he is cousin; otherwise it is not prime.

A number is called a prime when it has exactly two divisors, 1 and itself.

• Example

The number 12 is not prime, as the numbers that divide 12 are:

D(12) = 1,2,3,4.6 and 12

The number 17 is prime, as the divisors of 17 are:

D(17) = 1.17.

Prime numbers are used for various purposes in Mathematics.

Sieve of Eratosthenes

Finding prime numbers is not always an easy task. O method most used for this task is the sieve of Eratosthenes, which allows you to find all the prime numbers between two numbers.

Let's, for example, find the prime numbers from 1 to 100 using this method.

We will list all numbers from 1 to 100 in an organized way. Look:

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

We know that 1 has only 1 divisor, so it is not a prime. We also know that 2 has 2 divisors, 1 and itself, so 2 is prime. Now the others pair numbers they're all divisible by 2, so they're not primes. So let's mark all the other even numbers and the number 1 in the list.

From the numbers that are left in black, we know that 3 has only two divisors, so it is prime. However, the numbers multiples of 3, like the 6,9,12,15…, are not primes. We will now mark all numbers multiple of 3 that are left in the list.

We know that the number 5 is prime, but multiples of 5 (which are numbers ending in 5 or 0) are not, as 5 is a divisor of these numbers. So let's mark those numbers too.

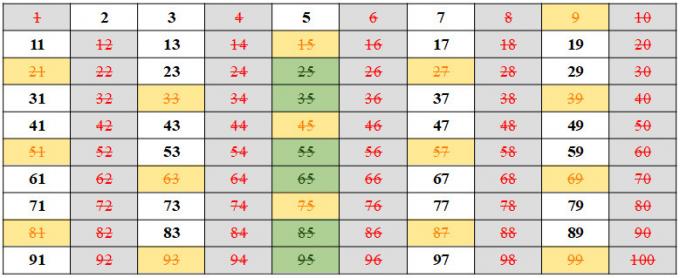
Number 7 is prime. Using the same reasoning, we will mark the multiples of 7 that have not yet been marked.

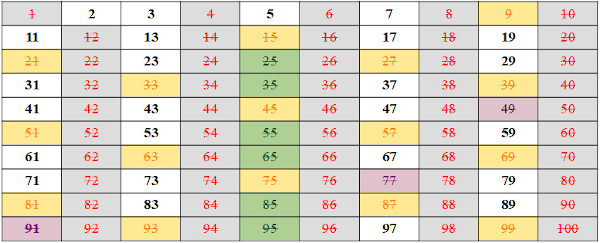
Now knowing that 11 is prime, let's look for the numbers multiple of 11, as there is no number multiple of 11, we know we've finished the sieve.

The remaining numbers are primes, so the primes from 1 to 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.

Observation: If we want to find the primes between larger numbers, like the primes from 1 to 200 or from 1 to 500, the process will continue until we find a prime number that has no multiple to strike out in the table.

See too: Divisibility criteria - processes that facilitate the division operation

Factorization

A number that is not prime can be factored, that is, we can perform what we call a prime factor decomposition. This process is useful for calculating the MMC it's the MDC.

To do the decomposition, we'll do successive divisions of the number until we get 1.

• Example

So the decomposition of 72 into prime factors is 2³.3².

Prime numbers from 1 to 1000

Know all prime numbers that exist between 1 and 1000.

2	3	5	7	11	13	17	19	23	29	31	37	41	43
47	53	59	61	67	71	73	79	83	89	97	101	103	107
109	113	127	131	137	139	149	151	157	163	167	173	179	181
191	193	197	199	211	223	227	229	233	239	241	251	257	263
269	271	277	281	283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409	419	421	431	433
439	443	449	457	461	463	467	479	487	491	499	503	509	521
523	541	547	557	563	569	571	577	587	593	599	601	607	613
617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863	877	881	883	887
907	911	919	929	937	941	947	953	967	971	977	983	991	997

solved exercises

Question 1 - Is the prime factor decomposition of the number 720 equal to?

A) 2³. 3². 5

B)2². 3³. 5

C) 2. 3. 5

D)2². 3. 5³

Resolution

Alternative A.

By carrying out the factorization, we have to:

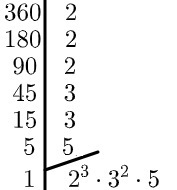
Question 2 -Check the correct statement:

A) Every odd number is prime.

B) Every even number is not prime.

C) 2 is the only even number that is prime.

D) 9 is the only odd number that is not prime.

Resolution

Alternative C.
a) False, as there are odd primes and non-prime numbers. For example, 3 is prime, but 15 is not.

b) False, as there is a single even number that is prime, the number 2.

c) True, as 2 is the only even number that is prime.

d) False, as there are several other odd numbers that are not prime, such as 15 mentioned, 21, 39, among others.