Imagine that you went to the market, bought a lot of fruit and now you need to organize it in your home. The purchased fruits were banana, apple, orange, lemon, watermelon, melon, guava and grape. Although they are all fruits, they are not all the same and you need to choose some pattern to be able to separate them into groups. Some of the fruits have a circular shape and, among them, there are large circular fruits (watermelon and melon) and others that are smaller (orange, lemon, apple, guava and grape). Also, within the group of smaller circular fruits, there are some that are citrus (orange and lemon). If we were to keep these fruits, separating them by groups, we would have:
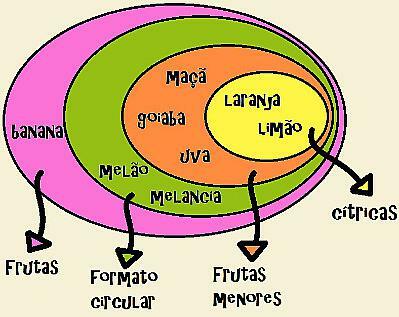
Organization of fruits according to type
Observing the image, it is possible to observe that the group of citrus fruits is within the other groups, as they have the same characteristics as other fruits. The same does not happen with the banana, which belongs only to the group of fruits, as it does not fit either with circular-shaped fruits or with smaller circular fruits or even with citrus fruits.
Something very similar happens with numbers. As there are many different types, they can be organized into different number sets according to their characteristics.
The first and simplest is the set of Natural Numbers, whose symbol is
. This group was originated by the need to count objects and it is formed by the first numbers created. We represent the elements of the set of natural numbers as follows:
= {0, 1, 2, 3, 4, 5, ...}
This is a set that is characterized by having an initial value (zero) and not having a final value. For this reason, we say that the set of natural numbers is infinite. We can also represent the natural numbers using the following line:
Representing natural numbers using a number line
After the natural numbers, there is the set of Integers, which is represented by 
. We use the letter z by virtue of the German word zahl, which means “numbers”. The set of integers is composed of all the elements of the natural set and also by these same elements preceded by the "minus" sign, the so-called "negative numbers”. We can represent the set of natural numbers as follows:
= {…, – 3, – 2, – 1, 0, 1, 2, 3, ...}
Note that the only number that does not receive the negative sign is zero. This set is also infinite, as we cannot determine its first or last element. Using the number line, we have the following representation for whole numbers:
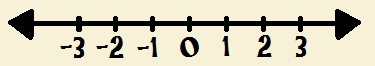
Representing whole numbers using the number line
We still have the set of Rational Numbers, represented by 
. The letter what is used in reference to the word "quotient" (the result of a division). This is because the set of rational numbers is made up of numbers that are the result of divisions. Let's look at some examples:
4: 2 = 2 
– 10: 5 = – 2
1: 2 = ½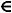
– 3: 4 = – ¾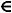
5: 3 = 1,666...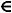
3: (– 6) = – 0,5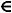
Therefore, in the set of rational numbers, we have the same elements found in the sets of naturals and integers, in addition to fractional numbers, decimals and periodic tithes. We can then represent the set of rational numbers as:
= {…, – 1, – ¾, – ½, 0, ½, ¾, 1, …} or simply,
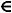
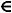
= {P/what | P , what , q 0}
A very special numerical set and different from the others is the set of irrational numbers, represented by 
. These numbers are infinite decimals that are not the result of divisions, but that can be the result of square root, for example, as is the case with the number √2 = 1,414213... The decimal part of irrational numbers has no periodicity. The set of irrational numbers does not cover the other sets.
Finally, we have the set of real numbers, represented by 
. Real numbers encompass all other sets described above.
Remember how we organized the fruits at the beginning of the text? Let's establish the relationship between the number sets in a very similar way:
Representation of the relationship between numerical sets
By Amanda Gonçalves
Graduated in Mathematics
Related video lessons:
