Fraction simplification is a way of writing the same fraction, but in such a way that numerators and denominators are written with smaller numbers. When we simplify a fraction, we find an equivalent fraction, but in reduced form.
Mathematics was generated from the desire to simplify situations and events in life. For this, methods were found to calculate distances, add objects, measure angles, discover unknown values, all in favor of the development of society.
Remember how equivalent fractions are found? If not, check out this article. equivalent fractions to better understand the process of simplifying fractions.
As said before, when we simplify a fraction, we are not changing it, we are just getting an equivalent fraction, that is, a fraction equal to the previous one.
To simplify a fraction, we must look at the numbers in the numerator and denominator and find some whole number that exactly divides the two numbers. To better understand this process, let's look at an example:

You could, in principle, find the number 2 that divides the numerator and want to simplify this fraction by 2, but remember that the chosen number must also divide the denominator. And in this case, the 2 doesn't divide the number 9.
And the number 3, would it exactly divide the numerator and denominator?
6 divided by 3 results in 2, and there is no remainder left, that is, it is an exact division.
9 divided by 3 results in 3 and there is no remainder, also an exact division.
With that, we find a first number that we can use in our simplification.

Note that the fraction we get is a fraction equivalent to our first fraction, and the numerator and denominator were written in reduced numbers.
You can repeat this process until you cannot have a number that divides the numerator and denominator. In our first example we cannot simplify again.
Let's look at another example:
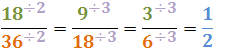
See that we perform the simplification three consecutive times, until we get a totally reduced fraction, totally simplified.
Note that with each simplification made the numerators and denominators were reduced, this is due to the fact that we are getting equivalent fractions through division and not multiplication.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Take the opportunity to check out our video lesson on the subject: