Polygons enrolled are those that are inside a circumference, so all its vertices are points of it. already the polygonscircumscribed are on the outside of a circumference and present all their sides tangents to her. Look at the following images:
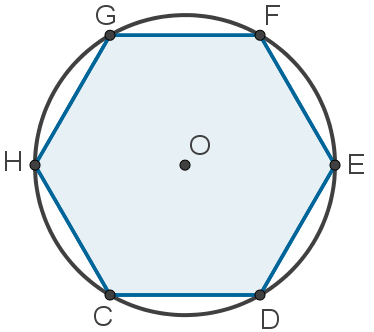
See that all vertices of the hexagon above are also points belonging to the circumference around you. It is in this situation that we say that the hexagon is inscribed on the circle or that the circle circumscribe O polygon.
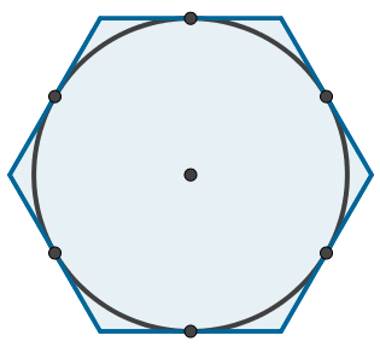
In this second image, it's the polygoncircumscribing the circumference. We can also say, in this case, that the circle is inscribed in the polygon. Note that for this, all sides of the polygon are tangent to the circle.
Elements of the inscribed regular polygon
Center of regular polygon
It is the center of the circle where this polygon is subscribed. It can be found from the meeting point between two bisectors from different sides of the polygon.
regular polygon radius
It is the element that starts from the center of a regular polygon to one of its vertices and has the same measure as the radius of the
circumference in which the regular polygon is inscribed.Apothem
It's the straight segment that connects the center of a polygonregular to the midpoint of one of its sides. the apothema always forms a anglestraight with the side of the polygon she touches.

Example of center, radius and apothema of regular polygon
In this image, r it's the damn polygonregularregistered, the point O is its center and the segment The it is apothema.
properties
The following properties are only valid for polygonsregular, that is, polygons that have all sides with the same measure and all angles congruent.
1 - All polygonregular Can be registered in a circumference;
2 – Every regular polygon can be circumscribed in a circle;
3 – The bisector the sides of a regular polygon meet on the center of the circumference that circumscribes it;
In other words, if a polygonregular is inscribed on a circle, the bisectors of its sides meet at the center of the circle, also called the center of the inscribed polygon. The following image illustrates this situation:
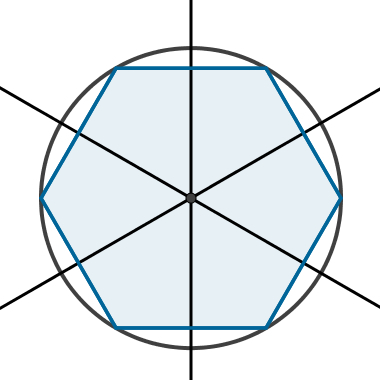
4 – In one polygonregularregistered on a circle, all the central angles, whose sides are formed by two consecutive radii of the inscribed regular polygon, are congruent. In addition, you can determine your measurement by dividing 360° by the number of sides of the polygon.

Angle whose sides are consecutive radii of the inscribed regular polygon
By Luiz Paulo Moreira
Graduated in Mathematics
Take the opportunity to check out our video lesson on the subject: