Newton's laws are a set of three laws that explain the dynamics of the movement of bodies, together they form the bases of classic mechanics. They were created by Isaac Newton and published in 1687, in his book "Mathematical Principles of Natural Philosophy".
These laws explain the causes that alter the state of motion of a body. A body can be in balance or it can be moving with some acceleration.
There are two equilibrium states: static and dynamic. When a body is in static equilibrium, it is at rest. When he's in dynamic equilibrium, he's moving in a straight line at a constant speed - uniform straight motion (MRU).
To get out of the equilibrium state, it is necessary that a force acts on the body and that it gains acceleration. We can understand force as an interaction between two bodies.
Newton's First Law: Law of Inertia
Every body remains in its state of rest or of uniform motion in a straight line, unless it is forced to change that state by forces applied to it.
The law of inertia explains that a
body tends to keep itself in balance, unless a non-zero net force is applied to it. The resulting force is the vector sum of all the forces acting on a body.If the sum of these forces is zero, that is, if the different forces cancel each other out, the body will remain in equilibrium: rest or uniform rectilinear movement. If the resulting force is non-zero, the body gains acceleration and leaves the equilibrium state.
According to this law, the greater the mass of a body, the greater its inertia and, therefore, the greater the force to take the body out of the state of rest or uniform rectilinear movement.
A simple example to understand the law of inertia is a moving bus that suddenly brakes. At this point, people standing inside the vehicle will be projected forward, as their body tends to keep moving.
The opposite happens when a stationary vehicle is accelerated quickly. In this case, people inside the vehicle are pushed backwards, as they tend to remain at rest.
Learn more about Newton's first law and inertia.
Newton's Second Law: Fundamental Principle of Dynamics
The change in motion is proportional to the imprinted driving force, and is produced in the straight-line direction in which that force is applied.
When applying a nonzero net force on a body, this one will win acceleration and will come out of rest or uniform straight motion (MRU) state.
The acceleration caused on the object is proportional to the force (f) applied to it. This means that the greater the force, the greater the movement of the body. Acceleration (a) and mass (m), on the other hand, are inversely proportional, as the greater the mass, the lower the acceleration.
This law is described by the following expression:
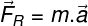
Force and acceleration are represented with an arrow, as they are vector quantities, that is, they have magnitude, direction and direction. According to this law, the resulting force produces an acceleration in the object in the same direction and direction.
Force is measured in Newton (N), which represents the force required to produce 1m/s² of acceleration in a 1000 gram body.
This law is also called Principle of Superposition of Forces, because the resulting force is calculated by the vector sum of all the forces acting on the body.
Learn more about Newton's second law.
Newton's Third Law: Law of Action and Reaction
To every action there is always an opposite reaction of equal intensity: the mutual actions of two bodies on each other are always equal and directed in opposite directions.
According to Newton's third law, whenever a force acts on a body, that body reacts with the same force and the same direction, but in the opposite direction. This means that if a force is applied from left to right, the body's reaction will be right to left.
From this law, it is understood that for the emergence of a force, it is necessary to interaction between two bodies, it is not possible that the action and reaction occur in the same body.
An example of the law of action and reaction is a person on skates pushing a very heavy object. In this case, the person will be propelled in the opposite direction and he will move due to the small frictional force between the ground and the roller skates.
See too Newton's third law, dynamics and strength.

