Meaning of Truth Table (What it is, Concept and Definition)

Truth table or truth table is a mathematical tool widely used in the field of logical reasoning. Its objective is to verify the logical validity of a compound proposition (argument formed by two or more simple propositions).

Examples of composite propositions:

• John is tall and Mary is short.
• Peter is tall or Joana is blonde.
• if Peter is tall, then Joan is a redhead.

Each of the above composite propositions is formed by two simple propositions joined by the bold connectives. Each simple proposition can be true or false and this will directly imply the logical value of the compound proposition. If we adopt the phrase "John is tall and Mary is short”, the possible valuations of this statement will be:

• If John is tall and Mary is short, the phrase “John is tall and Mary is short” is TRUE.
• If John is tall and Mary is not short, the phrase “John is tall and Mary is short” is FALSE.
• If John is not tall and Mary is short, the phrase “John is tall and Mary is short” is FALSE.
• If John is not tall and Mary is not short, the phrase “John is tall and Mary is short” is FALSE.

The truth table outlines this same reasoning (see topic Conjunction below) more directly. In addition, truth table rules can be applied. regardless of the number of propositions in the sentence.

How it works?

First, turn the question's propositions into symbols used in logic. The list of universally used symbols is:

Symbol	Logical Operation	Meaning	Example
P	.	Proposition 1	p = John is tall.
what	.	Proposition 2	q = Mary is short.
~	Denial	no	If John is tall, "~p" it's fake.
^	Conjunction	and	P^what = John is tall and Mary is short.
v	Disjunction	or	Pvq = John is tall or Mary is short.
→	Conditional	if then	P→what = If John is tall then Mary is short.
↔	biconditional	if and only if	P↔q = John is tall if and only if Mary is short.

Then, a table is assembled with all the valuation possibilities of a compound proposition, replacing the statements with symbols. It is worth clarifying that in cases where there are more than two propositions, they may be symbolized by the letters r, s, and so on.

Finally, the logical operation defined by the connector shown is applied. As listed above, these operations can be: negation, conjunction, disjunction, conditional and biconditional.

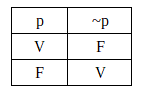
Denial

Denial is symbolized by ~. The logical operation of negation is the simplest and often does not require the use of the truth table. Following the same example, if John is tall (p) saying that John is not tall (~p) is FALSE, and vice versa.

Conjunction

The conjunction is symbolized by ^. The example "John is tall and Mary is short" will be symbolized by "p^q" and the truth table will be:

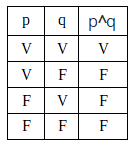
The conjunction suggests an idea of ​​accumulation, so if one of the simple propositions is false, it is impossible for the composite proposition to be true.

Conclusion: the conjunctive compound propositions (containing the connective and) will only be true when all of its elements are true.

Example:

• Paulo, Renato and Túlio are kind and Carolina is funny. - If Paulo, Renato or Túlio are not kind or Carolina is not funny, the proposition will be FALSE. It is necessary that all the information is true for the composite proposition to be TRUE.

Disjunction

The disjunction is symbolized by v. Changing the connective from the example above to or we will have "John is tall or Mary is short". In this case, the phrase will be symbolized by "pvq" and the truth table will be:

The disjunction implies an idea of ​​alternation, therefore, it is enough that one of the simple propositions is true for the composite one to be also true.

Conclusion: the disjunctive compound propositions (which contain the connective or) will only be false when all its elements are false.

Example:

• My mother, father or uncle will give me a present. - For the statement to be TRUE, it is enough that only one among the mother, father or uncle gives the gift. The proposition will only be FALSE if none of them give it.

Conditional

The conditional is symbolized by →. It is expressed by the connectives if and then, which interconnect the simple propositions in a causal relationship. The example "If Paulo is from Rio de Janeiro, then he is Brazilian" becomes "p→q" and the truth table will be:

Conditionals have an antecedent proposition and a consequent one, separated by the connective then. In the analysis of conditionals, it is necessary to evaluate which cases the proposition it may be possible, considering the relationship of implication between the antecedent and the consequent.

Conclusion: Conditional compound propositions (containing the connectives if and then) will only be false if the first proposition is true and the second false.

Example:

• If Paulo is from Rio, then he is Brazilian. - For this proposition to be considered TRUE, it is necessary to evaluate the cases in which it is POSSIBLE. According to the truth table above, we have:

1. Paulo is from Rio / Paulo is Brazilian = POSSIBLE
2. Paulo is from Rio de Janeiro / Paulo is not Brazilian = IMPOSSIBLE
3. Paulo is not from Rio / Paulo is Brazilian = POSSIBLE
4. Paulo is not carioca / Paulo is not Brazilian = POSSIBLE

biconditional

The biconditional is symbolized by ↔. It is read through the connectives if and only if, which interconnect the simple propositions in an equivalence relation. The example "John is happy if and only if Mary smiles." becomes "p↔q" and the truth table will be:

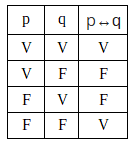
Biconditionals suggest an idea of ​​interdependence. As the name demonstrates, the biconditional is composed of two conditionals: one that starts from P for what (P→q) and another in the opposite direction (q→P).

Conclusion: At biconditional compound propositions (containing the connectives if and only if) will only be true when all propositions are true, or all propositions are false.

Example:

• João is happy if and only if Maria smiles. - Means to say that:

1. If John is happy, Mary smiles and if Mary smiles, John is happy = REAL
2. If John is not happy, Mary is not smiling and if Mary is not smiling, John is not happy = REAL
3. If João is happy, Maria does not smile = FALSE
4. If João is not happy, Maria smiles = FALSE

Overview

It is common for truth table scholars to memorize the conclusions of each of the logical operations. To save time when resolving issues, always keep in mind that:

1. Conjunctive Propositions: They will only be true when all elements are true.
2. Disjunctive Propositions: It will only be false when all elements are false.
3. Conditional Propositions: They will only be false when the first proposition is true and the second false.
4. Biconditional Propositions: It will only be true when all elements are true, or all elements are false.