Arithmetic Progression, also known as P. A, is a type of numerical sequence studied by Mathematics, where each term or element starting from the second is equal to the sum of the previous term with a constant.
In this type of numerical sequence, the number is always called the ratio (represented by the letter r) and it is obtained by the difference of one term in the sequence by its previous one.
Then, starting from the second element of the sequence, the numbers will all result from the sum of the constant with the value of the previous element.
For example, the sequence 5,7,9,11,13,15,17 can be characterized as an arithmetic progression, as its elements are formed by the sum of its predecessor with the constant 2.
Types of Arithmetic Progressions
To better understand this concept, below are examples of what are considered types of arithmetic progressions.
- (5,5,5,5,5...an) Finite PA of 0 ratio
- (4,7,10,13,16...an...) Infinite PA of ratio 3
- (70,60,50,40,30...an) Finite PA of ratio -10
In the three examples, it is observed that to calculate the BP ratio, it is necessary to calculate the difference between one of the terms and the term that precedes it, as shown in the image below:
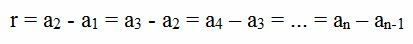
Formulas of the general term and the sum of an arithmetic progression
In this sense, the formula used that characterizes the general term of an AP is represented as follows:

Where do we have:
an = General term
a₁ = First term in the sequence.
n = Number of terms in P.A. or position of numerical term in P.A.
r = reason
However, if we have any finite P.A, to add its terms (elements) we will arrive at the following formula to add the n elements of a finite P.A.

Where do we have:
Sn = Sum of the first n terms of the PA
a₁ = First term of the PA
an = Occupies the nth position in the sequence
n = Term position
Classification of arithmetic progressions
As far as classifications are concerned, arithmetic progressions can be increasing, decreasing and constant.
A PA will be growing when its ratio (r) is positive, that is, greater than zero (r > 0). The numerical sequence will be increasing when each term from the second is greater than the predecessor. Ex: (1, 3, 5, 7, ...) is an increasing P.A of ratio 2.
The PA will be decreasing if its ratio (r) is negative, that is, less than zero (r < 0). The numerical sequence will be descending when each term from the second is smaller than the predecessor. E.g.: (15, 10, 5, 0, -5 ...) is a decreasing P.A of ratio – 5.
The PA will be constant when its ratio is null, that is, it is equal to zero (r = 0). All your terms will be the same. Ex: (2, 2, 2, ...) is a P.A constant with null ratio.
Arithmetic progression and geometric progression
Progressions are studied by mathematics to define real sequential numbers, however, there is a difference between arithmetic progression and geometric progression.
While the arithmetic progression presents the sequence of numbers where the numerical differences between a term and its antecedent is constant, in geometric progression the constant derives from the quotient of this term and its predecessor.
See also the meaning of Geometric progression.

