straight, semi-straight and straight segment are basic elements that constitute the studies of geometry. The idea of a straight line is very intuitive, we can have the notion of a straight line when we look at a string or a well-stretched wire.
The other two elements, ray and line segment, are parts of a line. The semi-straight is a “line with a beginning and without an end”. The segment is a “line with a beginning and an end”. Let's understand better about each of these elements?!
Index
- straight
- semi-rectal
- straight segment
- Relative positions of two lines
straight
One straight is a line formed by infinite aligned points, that is, a straight line is a line that has no beginning and no end.
It is impossible to draw a line as it is infinite. However, we can make a representation of a line, drawing just a piece of it. We use any lowercase letter to indicate it.
See some examples of straight line representation:

semi-rectal
One semi-straight it is a part of the straight line, it has a beginning, but it has no end. We use capital letters to indicate the starting point of the ray and a point through which this ray passes.
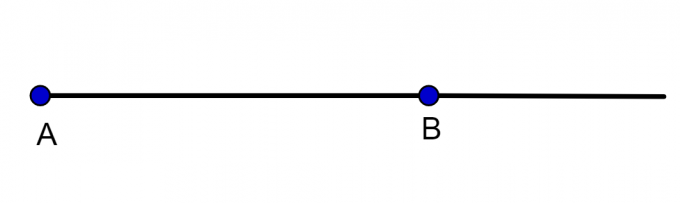
If the ray has no end, why do we need point B? Remember that through a single point A infinite straight lines pass. So point B serves to identify which ray we are talking about.
The notation for straight lines is: straight
straight segment
One straight segment it is a part of the straight line, it has a beginning and an end.
- Free Online Inclusive Education Course
- Free Online Toy Library and Learning Course
- Free Online Math Games Course in Early Childhood Education
- Free Online Pedagogical Cultural Workshops Course
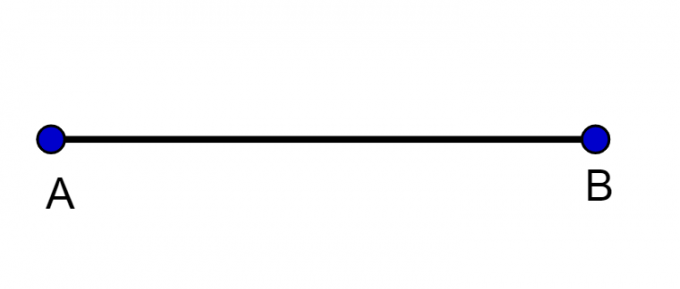
Here, points A and B are ends of the segment, that is, they represent the point where the segment starts and ends.
We use the following notation: line segment .
Relative positions of two lines
Two lines can be parallel, concurrent (or secant) or coincident.
Parallel lines: they are two straight lines that never cross.

Competing lines: are two straight lines that have a crossing point.

The crossing point is not always evident in the representation of two concurrent lines, as is the case of the lines and and f.
We must remember that the lines are infinite and imagine their continuity (dotted in the figure). If at any point these lines intersect, then they are competitors.
Coincident lines: they are two lines that occupy the same position, as if one were on top of the other.

You may also be interested:
- Flat Figure Areas
- Angles - Types, Classifications and Examples
- Planning of geometric solids
The password has been sent to your email.



