Exercises on the area of parallelograms

You parallelogramsthey are polygons four-sided, which have opposite sides parallel, two by two. Examples of parallelograms are: o square, O rectangle it's the diamond.

The area (A) of any parallelogram corresponds to the measure of its surface and can be determined by the following formula:

$\dpi{120} \mathbf{A = b \cdot h}$

On what:

B: measure of the base of the parallelogram;
H: height of the parallelogram.

To learn more about this subject, check out a list of exercises on the parallelogram area, with all resolutions of the issues.

Index

Exercises on the area of parallelograms
Resolution of question 1
Resolution of question 2
Resolution of question 3
Resolution of question 4

Exercises on the area of parallelograms

Question 1. Determine the area of the parallelogram with the dimensions shown in the figure below:

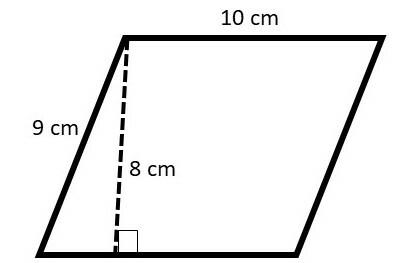
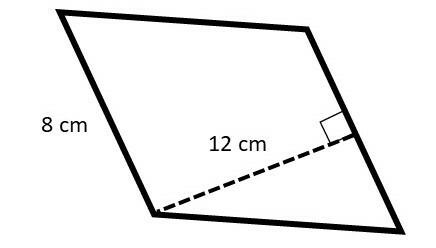
Question 2. Determine the area of the parallelogram with the dimensions shown in the figure below:

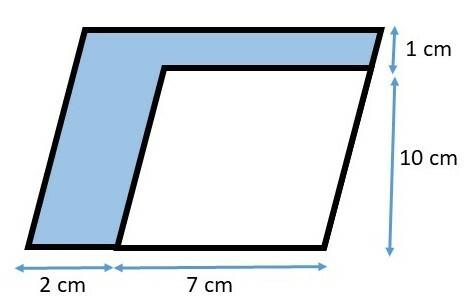
Question 3. Determine the colored surface area of the figure below:

Question 4. Determine the area of the parallelogram with dimensions shown in the figure below:

instagram story viewer

Resolution of question 1

We have b = 10 cm and h = 8 cm. Let's substitute these values into the parallelogram area formula:

$\dpi{120} \mathrm{A = b \cdot h}$

$\dpi{120} \Rightarrow \mathrm{A = 10 \cdot 8}$

$\dpi{120} \Rightarrow \mathrm{A = 80}$

Therefore, the parallelogram area is equal to 80 cm².

Resolution of question 2

We have b = 8 cm and h = 12 cm. Let's substitute these values into the parallelogram area formula:

$\dpi{120} \mathrm{A = b \cdot h}$

$\dpi{120} \Rightarrow \mathrm{A = 8 \cdot 12}$

$\dpi{120} \Rightarrow \mathrm{A = 96}$

Therefore, the parallelogram area is equal to 96 cm².

Resolution of question 3

The colored surface area corresponds to the area of the major parallelogram minus the area of the major parallelogram.

Let's calculate the area of each parallelogram separately.

Larger parallelogram:

We have b = 7 cm + 2 cm = 9 cm and h = 10 cm + 1 cm = 11 cm. Let's substitute these values into the parallelogram area formula:

$\dpi{120} \mathrm{A = b \cdot h}$

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

$\dpi{120} \Rightarrow \mathrm{A = 9 \cdot 11}$

$\dpi{120} \Rightarrow \mathrm{A = 99}$

Minor parallelogram:

We have b = 7 cm and h = 10 cm. Let's substitute these values into the parallelogram area formula:

$\dpi{120} \mathrm{A = b \cdot h}$

$\dpi{120} \Rightarrow \mathrm{A = 7 \cdot 10}$

$\dpi{120} \Rightarrow \mathrm{A = 70}$

So, the colored surface area is given by:

$\dpi{120} \mathrm{A_{colored} = A_{larger} - A_{smaller}}$

$\dpi{120} \Rightarrow \mathrm{A_{colored} = 99 -70}$

$\dpi{120} \Rightarrow \mathrm{A_{colored} = 29}$

Therefore, the colored surface area is equal to 29 cm².

Resolution of question 4

To calculate the area of the parallelogram, we need to determine the measure of its base, that is, the measure of the side. $\dpi{120} \overline{BC}$ .