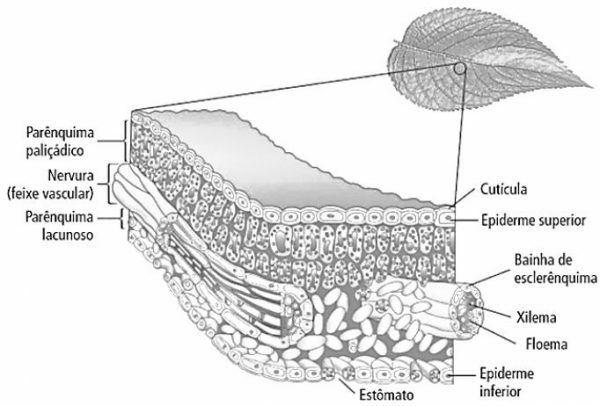
O determinant of a headquartersis a number obtainable for square matrices, which are matrices with the same number of rows and columns. Calculating the determinant is useful, for example, in problems involving systems of equations.
There are some ways to calculate the determinant of a matrix, in this post we will show you how to calculate this numerical value by Sarrus' method, also known as the diagonal method.
In a 1 x 1 matrix, the determinant is the only element in the matrix. So, let's see how to find the determinant for matrices of orders 2 and 3.
Determinant of a 2 x 2 matrix
Let's calculate the determinant of a matrix A of order 2 x 2.

First, we calculate the product between the main diagonal values (blue color) and the product between the minor diagonal values (red color). Note that 8 x (-3) = -24 and 7 x 15 = 105.

Finally, we subtract between these obtained values:
-24–105 = – 129
So, the determinant of matrix A is equal to -129.
- Free Online Inclusive Education Course
- Free Online Children's Learning and Toy Library Course
- Free Online Math Games Course in Early Childhood Education
- Free Online Pedagogical Cultural Workshops Course
Determinant of a 3 x 3 matrix
Let's calculate the determinant of a matrix A of order 3 x 3.

First, we must write the matrix and repeat the first and second columns:

Then we calculate the multiplication of the elements of each of the diagonals of the matrix, the main ones (blue color) and the secondary ones (red color). For example, see that 2 x 9 x (-6) = -108.
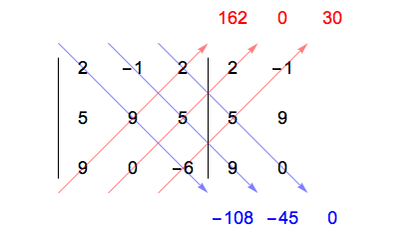
Finally, we add up all these values, but putting a negative sign on the secondary diagonal values (red color). Note that we put the minus sign before the parentheses.
-108 + (-45) + 0 – (162 + 0 + 30) = -345
By doing the calculation, we get the determinant of matrix A, which is equal to -345.
You may also be interested:
- Signs Rule
- Complex numbers
- List of Numerical Expression Exercises
- Trigonometric Functions - Sine, Cosine and Tangent
The password has been sent to your email.