Angle between two vectors

In math or physics, the vectors they are straight segments with direction, direction and length, which are used to represent quantities such as force, velocity and acceleration.

Vectors indicate trajectories and can be defined using a coordinate system (x, y). Considering the point (0,0) as the origin of the segment, the figure below shows a vector $\dpi{120} \boldsymbol{\vec{u}}$ whose end is the point $\dpi{120} \boldsymbol{ $x_1, y_1$}$ .

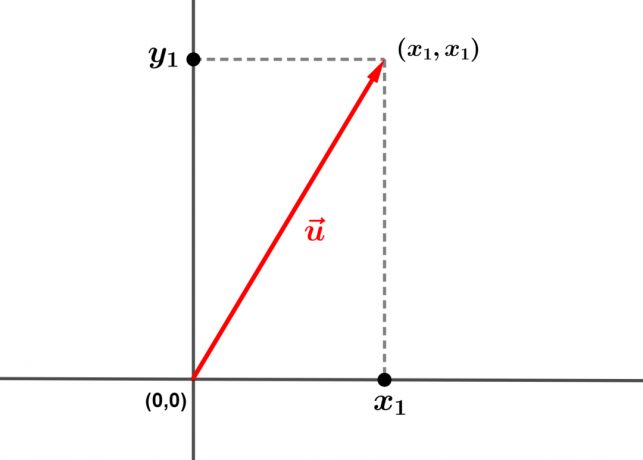
Notation: $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ .

the ordained $\dpi{120} \boldsymbol{x_1}$ is called the horizontal component and the abscissa $\dpi{120} \boldsymbol{y_1}$ , of vertical component.

Now consider, in addition to the vector $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ , another vector $\dpi{120} \boldsymbol{\vec{v}= $x_2, y_2$}$ and an angle formed between them, as shown in the figure below.

This angle between the vectors can be calculated by a formula that involves the dot product between the vectors and the norm (length) of each vector.

Angle between two vectors

Two vector dice $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ and $\dpi{120} \boldsymbol{\vec{v}= $x_2, y_2$}$ , the cosine of the angle $\dpi{120} \boldsymbol{\theta}$ among them is related to the internal product between the vectors and their standards as follows:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{\left \langle \vec{u}, \vec{v} \right \rangle}{\|\vec{u} \|.\| \vec{v} \| }}$

The numerator of the fraction is the inner product between the vectors, given by:

$\dpi{120} \boldsymbol{\left \lange \vec{u}, \vec{v} \, \right \rangle = x_1\cdot x_2+y_1\cdot y_2}$

And the denominator is the product between the standards of each of the vectors, as follows:

instagram story viewer

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

$\dpi{120} \boldsymbol{\|\vec{u}\|= \sqrt{(x_1)^2+ (y_1)^2}}$

$\dpi{120} \boldsymbol{\|\vec{v}\|= \sqrt{(x_2)^2+ (y_2)^2}}$

By making the replacement, we verified that the angle formula between two vectors é:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{x_1\cdot x_2+y_1\cdot y_2}{\sqrt{(x_1)^2+(y_1)^2} \cdot \sqrt{(x_2) )^2+(y_2)^2}}}$

Example:

Calculate the angle between the vectors $\dpi{120} \boldsymbol{\vec{u}= $2,4$}$ and $\dpi{120} \boldsymbol{\vec{v}= $5,3$}$ .

Applying the values in the formula, we have to:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{2\cdot 5+4\cdot 3}{\sqrt{(2)^2+(4)^2} \cdot \sqrt{(5 )^2+(3)^2}}}$

$\dpi{120} \Rightarrow \boldsymbol{cos\, \theta = \frac{10+12}{\sqrt{4+16} \cdot \sqrt{25+9}}}$

$\dpi{120} \Rightarrow \boldsymbol{cos\, \theta = \frac{22}{\sqrt{20} \cdot \sqrt{34}}}$

$\dpi{120} \Rightarrow \boldsymbol{\theta = cos^{-1}\left (\frac{22}{\sqrt{20} \cdot \sqrt{34}} \right ) }$

Using a calculator or a trigonometric table, we can see that:

$\dpi{120} \boldsymbol{ \theta = 32.47^{\circ}}$

You may also be interested:

Bows with more than one turn
Arcs and circular motion
trigonometric circle
speed of a vehicle

The password has been sent to your email.

Angle between two vectors

Angle between two vectors

Praise with the letter H

Praise with the letter F

Cheers with the letter C