Cone trunk: what is it, elements, formulas

O trunk of a cone is the solid formed by bottom of the cone when performing a section at any height parallel to the base. when we cut the cone at any given height, it is divided into two geometric solids, a cone smaller than the previous one and the trunk of a cone.

The trunk of the cone has specific formulas so that it is possible to calculate the total area and volume of this geometric solid.

Read too: What are Plato's solids?

Trunk cone elements

The trunk of a cone is formed when you make a section in a cone.

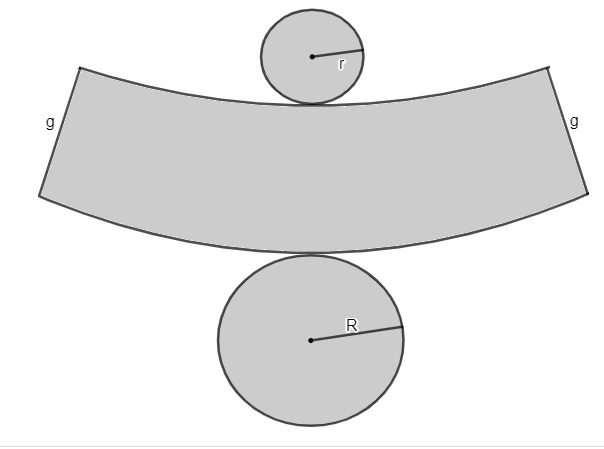
The trunk of a cone is a special case of round bodies. It gets its name because, in a cone, when we make a section parallel to the base, it is divided into two parts. The bottom part is the trunk of the cone.

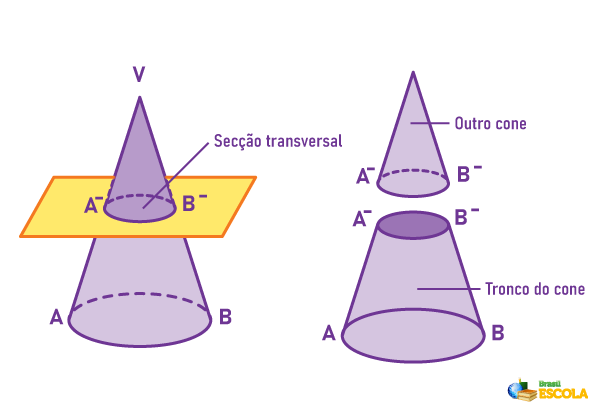
Given the trunk of a cone, there are important elements in this solid, which are given specific names.

R → radius of the largest base

h → cone height

r → radius of the smallest base

g → trunk cone generatrix

We can see that the trunk of the cone is composed of two faces in the shape of a circle

, which are known as bases. Furthermore, one of them always has a smaller radius than the other. Thus, r < R and, consequently, there is a larger base and a smaller base.

Do not stop now... There's more after the advertising ;)

Trunk Cone Generator

Given a cone trunk, it is possible calculate the generator value of this solid using the theorem of Pythagoras, when we know the radii of the largest and smallest base, in addition to the height.

g² = h² + (R – r) ²

Example:

Find the generatrix of a trunk cone that has a height equal to 8 cm, radius of base greater equal to 10 cm, and radius of base less than 4 cm.

To find the trunk of the cone generatrix, we have to:

h = 8
R = 10
r = 4

Substituting in the formula:

g² = h² + (R – r) ²
g² = 8² + (10 – 4)²
g² = 64 + 6²
g² = 64 + 36
g² = 100
g = √100
g = 10 cm

See too: How to find the center of a circle?

Trunk cone volume

To calculate the volume of the trunk of the cone, we use the formula:

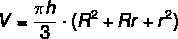
Knowing the height values, the radius of the largest base and the radius of the smallest base, it is possible to calculate the volume of the trunk of a cone.

Example:

Find the volume of a trunk cone that has a height equal to 6 cm, radius of the largest base equal to 8 cm, and radius of the smallest base equal to 4 cm. Use π = 3.1.

Planning the trunk of a cone

THE planing a geometric solid and the representation of your faces in a two-dimensional way. See below the plan of the trunk of the cone.

Total cone trunk area

Knowing the plane of a cone trunk, it is possible to calculate the value of the total area of ​​this geometric solid. We know that it is composed of two bases in the shape of a circle and also by its lateral area. The total area of ​​the trunk of a cone is the sum of the areas of these three regions:

THE_T = A_B + A_B + A_there

THE_T → total area

THE_B → larger base area

THE_B → smaller base area

THE_L → side area

Note that the bases are circles and that the side area starts from a circle, so:

THE_there = πg (R + r)

THE_B = πR²

THE_B = πr²

Example:

Calculate the total area of ​​the trunk of the cone that has a height equal to 12 cm, radius of base greater equal to 10 cm and radius of base less than 5 cm. Use π = 3.

First we will find the generatrix to calculate the lateral area:

g² = 12² + (10 – 5)²
g² = 12² + 5²
g² = 144 + 25
g² = 169
g = √169
g = 13

THE_there = πg (R + r)
THE_there = 3 · 13 (10 + 5)
THE_there = 39 · 15
THE_there = 39 · 15
THE_there = 585 cm²

Now we will calculate the area of ​​each of the bases:

THE_B = πR²
THE_B = 3 · 10²
THE_B = 3 · 100
THE_B = 300 cm²

THE_B = πr²
THE_B= 3 · 5²
THE_B= 3 · 25
THE_B= 75 cm²

THE_T = A_B + A_B + A_there
THE_T = 300+ 75 + 585 = 960 cm²

See too: What are the differences between circle and circumference?

solved exercises

Question 1 - (Enem 2013) A cook, expert in making cakes, uses a mold in the format shown in the figure:

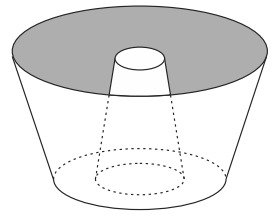
It identifies the representation of two three-dimensional geometric figures. These figures are:

A) a frustum of cone and a cylinder.

B) a cone and a cylinder.

C) a trunk of a pyramid and a cylinder.

D) two cone trunks.

E) two cylinders.

Resolution

Alternative D. Analyzing the geometric solids, the two have two circular faces of different sizes, so they are cone frustums.

Question 2 - (Nucepe) How it is and what a cup is primarily for, we all know: serving drinks, especially hot ones. But where did the idea of ​​creating a "glass with handle" come from?

The tea, which has an oriental origin, was initially served in round pots without handles. According to tradition, this was even a warning to those conducting the drinking ceremony: If the container burned your fingertips, it was too hot to drink. At the ideal temperature, it didn't bother, even with direct contact with the porcelain.

Source: http://www.mexidodeideias.com.br/viagem/a-historia-da-xicara. Accessed on 01/06/2018.

A teacup is shaped like a straight cone trunk, as shown in the figure below. What is the approximate maximum volume of liquid it can contain?

A) 168 cm³

B) 172 cm³

C) 166 cm³

D) 176 cm³

E) 164 cm³

Resolution

Alternative D.

To find the volume, let's first calculate the value of each of the rays. To do this, just divide the diameter by two.

R = 8/ 2 = 4

r = 4/2 = 2

In addition to the radius, we know that h = 6.

So, we have to:

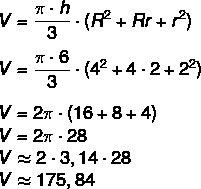
The closest value is 176 cm³.

By Raul Rodrigues de Oliveira
Maths teacher

Would you like to reference this text in a school or academic work? Look:

OLIVEIRA, Raul Rodrigues de. "Cone trunk"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/tronco-cone.htm. Accessed on June 28, 2021.