bridgeinWheatstone is a kind of electric circuit which can be used to measure, with great precision, the electrical resistance on one resistor unknown. These circuits consist of four resistors and a galvanometer. We say that the Wheatstone Bridge is at balance when there is no electric current flowing through the galvanometer.
O galvanometer it is one of the first devices used to measure electrical current. It is a measuring device that has a small needle, used to indicate the passage of electrical current through a coil that rotates, due to the interaction between the electrical current and the magnetic field produced by a small magnet.
Read too:Physics Curiosities
The figure below shows the schematic of a galvanometer. Watch:
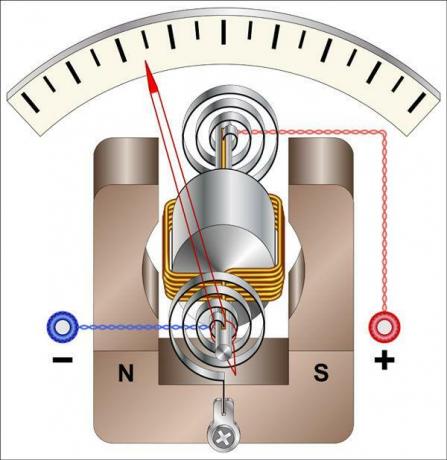
The galvanometer can be used to measure small electrical currents.
Despite its name, the Wheatstone Bridge was invented by SamuelHunterChristie, however, suffered great modifications and improvements by the hands of sirCharlesWheatstone, responsible for popularizing this type of circuit. Charles Wheatstone is also known for his famous invention, the
rheostat – a variable resistance resistor.Do not stop now... There's more after the advertising ;)
Of the four resistors that make up the Wheatstone bridge, two are known, one can be changed (variable resistance) and one is unknown. When connecting an unknown resistance to a Wheatstone bridge, adjust the value of the variable resistance until the galvanometer reports that there is no electric current passing through it.
The figure below shows what the Wheatstone bridge circuit looks like, note:

ig – current in the galvanometer
RX – unknown resistance
R1, R2, R3 – known resistances
Using the above circuit, it is possible to determine with great precision the value of resistance RX. Therefore, it is necessary that the Wheatstone bridge is in equilibrium, that is, the differentiation of electric potential among the branches CBA and ADB must be null, so that no current flows through the branch galvanometer CD.
According to Kirchhoff's second law, which concerns the conservationgivesenergy, we know that the sum of electrical potentials in a closed loop must be zero. Therefore, the sum of the mesh potentials formed by the nodes ADC and also from the mesh DBC must be equal to 0.
To calculate the electrical potentials in each of these branches, we'll use Ohm's law, so then using the rules and conventions established by Kirchhoff's laws and the circuit shown in the previous figure, we will have the following result:
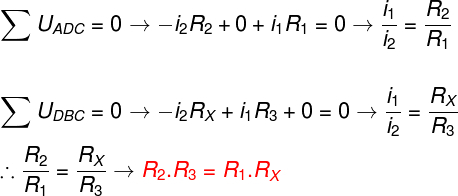
As a consequence of energy conservation, we can determine the unknown resistance by the cross product of the resistors.
After applying Kirchoff's laws to the meshes mentioned above, we conclude that it is possible to determine the modulus of the unknown strength through the cross product between the strengths. Another way to find the same result would be to admit that the potential drop between points A and C and points A and D are equal so that there is no electrical current flowing through the galvanometer.

Through the voltage drops, it is also possible to find the relationship between the cross products
Video Lesson: Wheatstone Bridge
applications
In addition to its common use - measuring unknown electrical resistances, the Wheatstone bridge can also be used in several types precision sensors such as scales, thermostats, pressure sensors, acceleration sensors, noise and motion detectors, etc.
Read too: Curiosities about electricity
solved exercises
1) A Wheatstone bridge, like the one shown in the figure below, is in balance when its three resistors, of resistance 10 Ω, 20 Ω and 30 Ω, are connected to a fourth resistance resistor unknown.

The alternative that presents the electrical resistance of the fourth resistor is:
a) 10 Ω
b) 20 Ω
c) 60
d) 40 Ω
e) 30 Ω
Resolution:
Template: Letter C
As the Wheatstone bridge is in equilibrium, we can say that the cross product of its resistances is equivalent. So, we will do the following calculation:
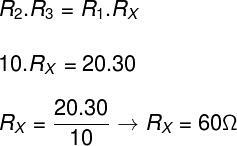
2) Determine the value of resistance R on the Wheatstone bridge shown below. Assume that the circuit is in equilibrium.
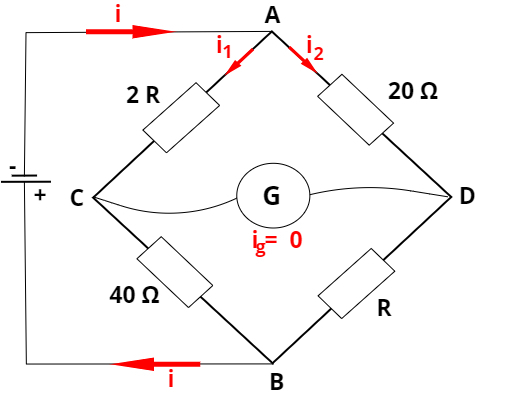
Resolution:
As the circuit is in equilibrium, we can use the cross product of the resistances. Thus, we should solve the following calculation:

By Me. Rafael Helerbrock
Would you like to reference this text in a school or academic work? Look:
HELERBROCK, Rafael. "Wheatstone Bridge"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/ponte-wheatstone.htm. Accessed on June 28, 2021.