THE 2nd degree equation is characterized for one polynomial of degree 2, that is, a polynomial of type ax2+bx+c, where The, B and ç they are real numbers. When solving an equation of degree 2, we are interested in finding values for the unknown. x that makes the value of the expression equal to 0, which are called roots, that is, ax2 + bx + c = 0.
Read too: Differences between function and equation
Types of 2nd Degree Equations
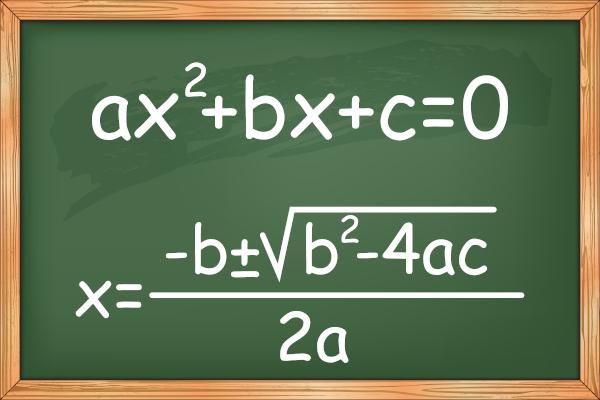
The 2nd degree equation can be represented by ax²+bx+c=0, where the coefficients The, B and ç are real numbers, with The ≠ 0.
→ Examples
a) 2x2 +4x – 6 = 0 → a = 2; b =4 and c = – 6
b) x2 – 5x + 2 = 0 → a =1; b= – 5 and c = 2
c) 0.5x2 + x –1 = 0 → a = 0.5; b = 1 and c = -1
The 2nd degree equation is classified as complete when all coefficients are different from 0, that is, The ≠ 0, B ≠ 0 and ç ≠ 0.
The 2nd degree equation is classified as incomplete when the value of the coefficients B or ç are equal to 0, that is, b = 0 or c = 0.
→ Examples
a) 2x2 – 4 = 0 → a = 2; b = 0 and c = – 4
b) -x2 + 3x = 0 → a = – 1; b = 3 and c = 0
c) x2 = 0 → a = 1; b=0 and c=0
Heads up: the coefficient value The it is never equal to 0, if that happens, the equation is no longer 2nd degree.
How to solve 2nd degree equations?
The solution of a 2nd degree equation occurs when the roots are found, that is, the values assigned to x. These values of x must make the equality true, that is, by substituting the value of x in the expression, the result must equal 0.
→ Example
Considering the x equation2 – 1 = 0 we have that x’ = 1 and x’’ = – 1 are solutions of the equation, because substituting these values in the expression, we have a true equality. Look:
x2 – 1 = 0
(1)2 – 1 = 0 and (–1)2 – 1 = 0
To find the solution of a equation, it is necessary to analyze whether the equation is complete and incomplete and select which method will be used.
Solution method for equations of type ax²+ c = 0
The method to determine the solution of incomplete equations that have B=0consists of isolating the unknown x, thus:

→ Example
Find the roots of the equation 3x2 – 27 = 0.

If you want to know more about this method, go to: 2nd degree incomplete equation with null coefficient b.
Solution method for equations of type ax2 + bx = 0
The method for determining the possible solutions of an equation with ç =0, consists of using the evidence factoring. Look:
ax2 + bx = 0
x·(ax + b) = 0
When looking at the last equality, it is noticeable that there is a multiplication and that for the result to be 0, it is necessary that at least one of the factors is equal to 0.
x·(ax + b) = 0
x = 0 or ax + b = 0
Thus, the solution to the equation is given by:

→ Example
Determine the solution of the equation 5x2 – 45x = 0

If you want to know more about this method, go to: incomplete 2nd degree equation with null coefficient c.
Solution method for complete equations
The method known as Bhaskara method or Bhaskara formula points out that the roots of a 2nd degree equation of type ax2 + bx + c = 0 is given by the following relationship:

→ Example
Determine the solution of the equation x2 – x – 12 = 0.
Note that the coefficients in the equation are: a = 1; B= – 1 and ç = – 12. Substituting these values in Bhaskara's formula, we have:

The delta (Δ) is named after discriminating and notice that it is inside a square root and, as we know, taking the real numbers into account, it is not possible to extract the square root of a negative number.
Knowing the value of the discriminant, we can make some statements about the solution of the 2nd degree equation:
→ positive discriminant (Δ > 0): two solutions to the equation;
→ discriminant equal to zero (Δ = 0): the solutions of the equation are repeated;
→ negative discriminant (Δ < 0): does not admit real solution.
Second Degree Equation Systems
When we simultaneously consider two or more equations, we have a system of equations. The solution of a 2-variable system is the set of ordered pairs which simultaneously satisfies all the equations involved.
→ Example
Consider the system:

With the values: x’ = 2, x’’ = – 2 and y’ = 2, y’’ = – 2 we can assemble ordered pairs that satisfy the system equations simultaneously. See: (2, 2), (2, – 2), (– 2, 2), (– 2, – 2).
Recall that an ordered pair is written of the form (x, y).
The methods for finding the solution of a system of equations are similar to that of linear systems.
→ Example
Consider the system:

From the equation x – y = 0, let's isolate the unknown x, thus:
x - y = 0
x = y
Now we must substitute the isolated value into the other equation, like this:
x2 – x –12 = 0
y2 – y –12 = 0
Using Bhaskara's method, we have to:

Since x = y, we will have x’ = y’ and x’’ = y’’. I.e:
x’ = 4
x’’ = -3
Thus, the ordered pairs are solutions of the system (4, 4) and (– 3,– 3).
read more: System of 1st and 2nd degree equations
solved exercises
question 1 – (ESPM -SP) The solutions to the equation below are two numbers
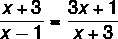
a) cousins.
b) positive.
c) negative.
d) pairs.
e) odd.
Solution
We know that the denominators of a fraction cannot be equal to zero, so x ≠1 and x≠3. And since we have an equality of fractions, we can cross-multiply, obtaining:
(x+3) · (x+3) = (x – 1) · (3x +1)
x2 + 6x +9 = 3x2 – 2x – 1
x2 – 3x2 + 6x + 2x +9 +1 = 0
(– 1) – 2x2 + 8x +10 = 0 (– 1)
2x2 – 8x – 10 = 0
Dividing both sides of the equation by 2, we have:
x2 – 4x – 5 = 0
Using Bhaskara's formula it follows that:

Note that the roots of the equation are odd numbers.
Alternative e.
question 2 – (UFPI) A poultry farmer found that after placing (n +2) birds in each of the n available aviaries, only one bird would be left. The total number of birds, for any natural value of n, is always
a) an even number.
b) an odd number.
c) a perfect square.
d) a number divisible by 3.
e) a prime number.
Solution
The number of birds can be found by multiplying the number of aviaries by the number of birds placed in each one. of them, by the statement of the exercise after doing this process there is still one bird left, we can write all this in the following manner:
n·(n+2) +1
Performing the distributivity we will obtain:
no2 + 2n +1
And factoring this polynomial it follows that:
(n+1)2
Thus, the total number of birds is always a perfect square for any natural number n.
Alternative C
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/equacao-2-grau.htm