THE planning on one geometric solid it is the presentation of all the shapes that constitute its surface in a plane, that is, in two dimensions. These plans are used in various ways, such as to calculate the area of the surface of a solid.
Check out the plans From solidsgeometric known and a way to calculate the area of the solid from its flatness.
Pyramid
At pyramids are solids formed by a base, which can be any polygon, and by side faces that are obligatorily triangles. The planning of pyramid it will always have a polygon and some triangles.

Most common planning of a pyramid with a pentagonal base
Note that the number of sides of the base of a pyramid is equal to the number of triangles that appear on your planning. Also note that triangles are not necessarily congruent (equal), which only happens when the base polygon is regular.
Prisms
You prisms are geometric solids formed by two bases, which are any congruent and parallel polygons, and by lateral faces that are always parallelograms.
In prisms, the number of side faces is also equal to the number of sides of one of its bases. So your
planning always presents two congruent polygons and some parallelograms, which will only all be the same if the bases of the prism are regular.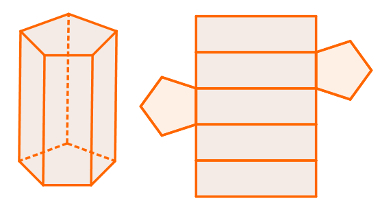
Most common planning of a pentagonal base prism
A way to calculate the area of prisms, in addition to solved examples, can be found on here.
cones
You cones are geometric solids formed by a circle, which is its base, and by a curved surface in the shape of a funnel. The two geometric figures resulting from the planning of a cone are a circular sector and a circle. Look:
Do not stop now... There's more after the advertising ;)
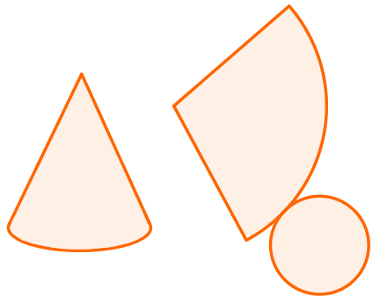
The area of the cones can be found by the following expression:
A = πr (g + r)
In the formula, r is the lightning of the cone and g is the generatrix. More details about this formula can be found on here. See an example calculation:
What is the area of a cone whose generatrix measures 10 cm and the radius is 5 cm?
Solution: replace this data in the formula above and assume π = 3.14.
A = πr (g + r)
A = 3.14·5(10 + 5)
A = 15.7·15
H = 235.5 cm2
cylinders
You cylinders they are geometric solids whose bases are two parallel and congruent circles. In your planning, we have two circles and a rectangle. Look:
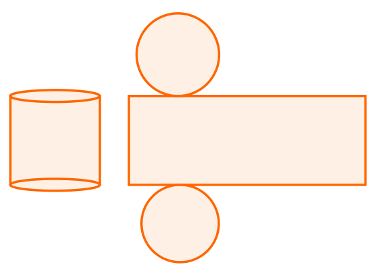
THE area of cylinder is determined by the sum of the areas of the two bases and the lateral surface. Knowing that these figures are two congruent circles and a rectangle, we can perform the following sum:
A = 2AÇ + AR
A = 2πr2 + bh
In this formula, r is the radius of the cylinder, H is your height and B is the base of the rectangle obtained in the unfold. This base is exactly the length of the circle: 2πr.
A = 2πr2 + 2πrh
A = 2πr (r + h)
See an example of area calculation:
A cylinder has a circular base whose radius is 2 cm and the height is 10 cm. Calculate your area.
Solution: replacing the given values in the formula above and considering π = 3.14, we will have:
A = 2πr (r + h)
A = 2·3.14·2·(2 + 10)
A = 12.56·12
H = 150.72 cm2
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Planning of geometric solids"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/planificacao-solidos-geometricos.htm. Accessed on June 27, 2021.
Math

Learn more about the cylinder, three-dimensional geometric form, and get to know the formal definition and classifications of this geometric solid. Also learn which are the cylinder sections, which can be transverse or meridional. See also how sections can be used to arrive at the cylinder volume formula.


