Balancestatic is the condition in which the resultant of forces and the sum of the moments of forces, or torques, are null. When in static equilibrium, bodies are at rest. Altogether, there are two three different types of balance: stable, unstable and indifferent.
Lookalso: Everything you need to know about Newton's laws
Static and dynamic balance
Before we start, some concepts are of fundamental importance for us to understand this article, check them out:
- Strengthresulting: is calculated through the Newton's 2nd Law. In the equilibrium condition, the vector sum of these forces must be nil;
- Torque or moment of a force: it concerns the dynamic agent of rotation, that is, when a non-zero torque is applied to a body, it will tend to describe a rotational movement.
we call balance the situation in which a body, extended or punctual, is subject to a net resultant force. In this way, and in accordance with what is established by the Newton's 1st Law, known as the law of inertia, a body in balance can be either at rest or in
uniform rectilinear movement — situations that are called static equilibrium and dynamic equilibrium, respectively.Types of static equilibrium
- Unstable balance: when a body undergoes a small displacement from its equilibrium position, however small, it will tend to move further and further away from that position. Look at the figure below:

- Stable balance: when a body, displaced from its balanced position, tends to return to its initial position, as in the case shown in this figure:

- Balanceindifferent: when a body, regardless of where it is positioned, remains in balance, check:
know more: Discover how the soccer ball curves in the air
Balance of the material point and balance of the extended body
When the dimensions of a body can be neglected, as in the case of a small particle, for example, we talk about balanceofScorematerial. In these cases, for the body to be in balance, it is enough that the sum of the forces acting on it is nil.
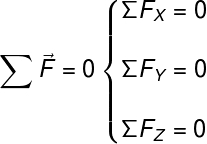
F - strength
FX – x component of forces
Fy – y component of forces
did – z component of forces
The figure indicates that the sum of the forces and the sum of the components of the forces in each direction must be equal to zero, so that the point symmetry body is in static equilibrium.
Do not stop now... There's more after the advertising ;)
When it is not possible to disregard the dimensions of the body, as in the cases of bars, drawbridges, supports, levers, gears and other macroscopic objects, one speaks of balanceofbodyextensive. In order to correctly define this type of balance, it is necessary to take into account the distance between the point of application of a force to the axis of rotation of these bodies, in other words, the condition of static or dynamic equilibrium requires that the sum of torques (or moments) be null, as occurs with forces applied.
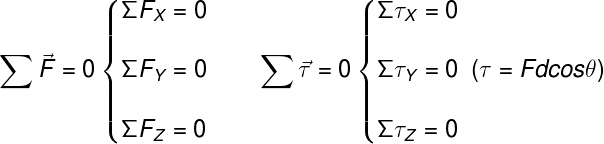
The above conditions indicate that, in the case of an extended body, it is necessary that the sum of forces and torques is zero in each direction.

Solved exercises on static balance
Solving static balance exercises requires a basic knowledge of sum. vector and vector decomposition.
Accessalso: Are you having difficulties? Learn how to solve exercises using Newton's laws
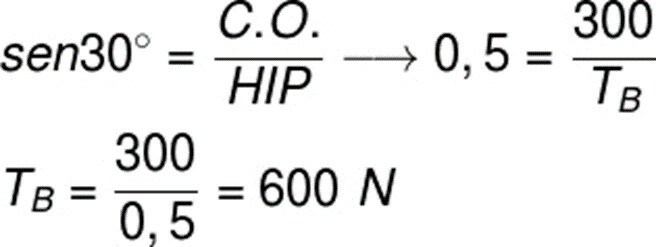
Question 1)(Isul) A box A, weighing 300 N, is suspended by two ropes B and C as shown in the figure below. (Data: sin 30º = 0.5)

The value of the pull on string B is equal to:
a) 150.0 N
b) 259.8 N
c) 346.4 N
d) 600.0 N
Template: Letter D
Resolution:
To solve this exercise, we have to use the trigonometry, in order to calculate the pull on string B. For this, it is necessary that we use the definition of sine, as the angle formed between the strings is 30º, and the sine formula indicates that it can be calculated by the ratio between the opposite side and the hypotenuse. See the next figure, in it we form a triangle with the vectors TB (pull on rope B) and weight (P):
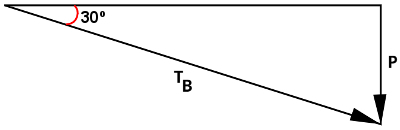
Based on it, we must make the following calculation:
Question 2)(Speck) A block with mass m = 24 kg is kept suspended in balance by the inextensible and negligible mass L and Q strings, as shown in the following figure. Rope L forms a 90° angle with the wall and rope Q forms a 37° angle with the ceiling. Considering the acceleration due to gravity equal to 10m/s², the value of the traction force that the rope L exerts on the wall is:
(Data: cos 37° = 0.8 and sin 37° = 0.6)

a) 144 N
b) 180 N
c) 192 N
d) 240 N
e) 320 N
Template: Letter e
Resolution:
First, we must determine what is the value of the traction supported by the Q cable, for that, we use the sine ratio, as in the previous exercise:

After we have found the tension in wire Q, we must calculate the component of this tension that is canceled by the tension exerted by cable L. Now, we'll use the cosine of the angle, since the horizontal component of the pull on cable Q is the side adjacent to the 37° angle, note:
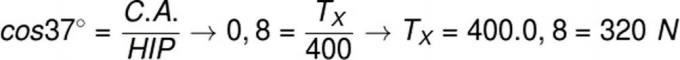
Question 3) (uerj) A man with a mass equal to 80 kg is at rest and balanced on a rigid board 2.0 m long, whose mass is much smaller than that of a man. The board is positioned horizontally on two supports, A and B, at its ends, and the man is 0.2 m from the end supported by A. The intensity of the force, in newtons, that the board exerts on support A is equivalent to:
a) 200
b) 360
c) 400
d) 720
Template: Letter D
Resolution:
We made a diagram so that you can view the exercise more easily, check it out:

As the bar on which the man is supported is an extensive body, one must take into account both the sumof theforces as to sumvectorFromtorques that act on it. Thus, we must make the following calculations:

To do these calculations, we first use the condition that states that the sum of the torques must be equal to zero, then, we multiply the forces with their distances from the axis of rotation of the rod (in this case, we choose position A). To determine the signals, we use the signalpositive for the torques that produce rotations in the sensecounter-clockwise, while the signal negative was used for the torque produced by the weight force, which tends to rotate the bar in the senseschedule.
The calculation of the resultant of the torques resulted in NB = 80 N, and then we use the second equilibrium condition. In this case, we say that the sum of the forces acting on the bar must be zero, and we get a normal reaction at point A equal to 720N.
By Rafael Hellerbrock
Physics teacher
