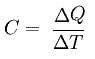In classical mechanics, circular motion consists of the movement of a particle on a circle with angular velocity. Bodies, such as artificial satellites, are good examples of particles that describe uniformly varying circular motion. Circular motion is classified into: uniform circular motion and uniformly varied circular motion.
artificial satellites they are man-made bodies placed in orbit around the Earth or any other planet.
Uniformly Varied Circular Movement
Circular movements are very common in everyday life. They are found on bicycles, motor vehicles, factories, equipment in general, etc.
When talking about circular motion, it is necessary to introduce angular properties such as angular acceleration, angular displacement and angular velocity. In the case of circular movements, there is also the definition of period, which is a property used in the study of periodic movements.
periodic movement is everyone who repeats identically at equal time intervals.
Uniformly varied circular motion is one that has variable velocity and constant angular acceleration is nonzero. Here acceleration is designated by the Greek letter gamma (γ) and angular velocity by the letter omega (ω). The equations that determine the MUCV are very similar to the uniformly varied rectilinear motion (MRUV). Comparing the equations that define the movements, we have:
Uniformly Varied Circular Movement
Linear Equations (MRUV) Angular Equations (MCUV)
 |
 |
 Do not stop now... There's more after the advertising ;) |
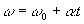 |
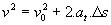 |
 |
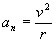 |
 |
Where:
θ and θ0 are, respectively, the final and initial position of the particle.
ω ω0 are, respectively, the final and initial angular velocity of the particle.
By Marco Aurélio da Silva
Brazil School Team
mechanics - Physics - Brazil School
Would you like to reference this text in a school or academic work? Look:
SANTOS, Marco Aurélio da Silva. "Uniformally Varied Circular Movement (MCUV)"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/movimento-circular-uniformemente-variado.htm. Accessed on June 27, 2021.