Polygons: elements, classification, nomenclature

Polygons are pictures flat geometrics and closed formed by straight segments. The polygons are divided into two groups, the convex and the not convex. When a polygon has all its sides equal and, consequently, all the angles internal equal, it is a polygon regular. Regular polygons can be named according to the number of their sides.

See too: Construction of circumscribed polygons

Elements of a polygon

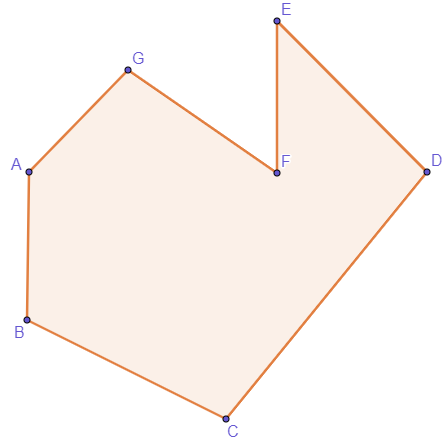
Polygon is a flat, closed figure formed by the union of a finite number of straight line segments. So, consider any polygon:

Points A, B, C, D, E, F, G and H are the vertices of the polygon and are formed by the meeting of segments AB, BC, CD, DE, EF, FG, GH and HA, called sides of the polygon.

The segments AF, AE, AD and BG are the diagonals of the polygon. (Note that these are some examples of diagonals, in the previous polygon we have more of these.) Diagonals are line segments that "connect" the vertices of the polygon.

Do not stop now... There's more after the advertising ;)

Nomenclature of a polygon

We can name the polygons according to their number of sides. See the name of the main polygons in the table below.

Number of sides (n)	Nomenclature
3	triangle
4	quadrangle
5	Pentagon
6	Hexagon
7	Heptagon
8	Octagon
9	Enneagon
10	Decagon
11	Undecagon
12	Dodecagon
15	Pentadecagon
20	Icosagon

Note that it is not necessary to decorate the table, but to understand it. With the exception of the triangle and the quadrilateral, the word formation is:

Number of sides + gono

For example, when we have the polygon of five sides, automatically remember the prefix penta plus the suffix gono: Pentagon.

Example

Determine the name of the following polygon:

The number of sides of the polygon is seven, so the polygon is a heptagon.

polygon classification

Polygons are classified by measure of your angles and sides. A polygon is said to be equilateral when it has congruent sides, that is, all sides are equal; and it will be called equiangle when it has congruent angles, that is, all equal angles.

If a polygon is equilateral and equiangle, then it will be a regular polygon.

In every regular polygon, the center is the same distance from the sides, that is, it is equidistant from the sides. The center of the polygon is also the center of the circle inscribed in the polygon, that is, the circumference which is "inside" the circumference.

Read more: Polygon similarity: see what the conditions are

Sum of internal angles of a polygon

Be the_i an interior angle of a regular n-sided polygon, we will represent the sum of these interior angles by S_i.

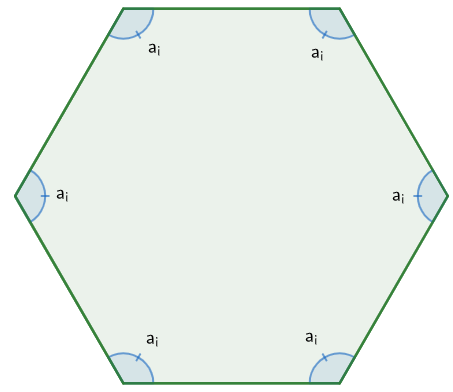
Thus, the sum of the internal angles is given by:

s_i = (n - 2) · 180°

To calculate the value of each inner angle, just take the sum of the inner angles and divide by the number of sides, ie:

The_i = s_i
no

Example 1

Find the sum of the interior angles and then the measure of each interior angle of an icosagon.

We know that an icosagon has twenty sides, so n = 20. Replacing in the relationships, we have:

s_i = (n - 2) · 180°

s_i = (20 - 2) · 180°

s_i = 18 · 180°

s_i = 3240°

Now, to determine the value of each internal angle, just divide the value found by the number of sides:

The_i = 3240°
20

The_i = 162°

Example 2

The sum of the interior angles of a regular polygon is 720°, find the polygon.

Replacing the statement information in the formula, we have:

720° = (n - 2) · 180°

720° = 180n - 360°

180n = 720° + 360°

180n = 1080°

n = 1080°
180°

n = 6 sides

Thus, the desired polygon is the hexagon.

Sum of outside angles of a polygon

The sum of the outside angles of a polygon is always equal to 360°.

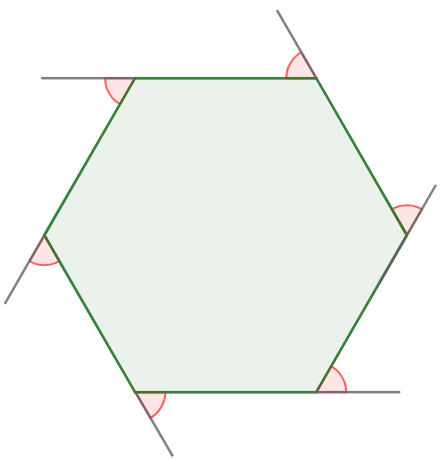
s_and = 360°

The_and = s_and
no

The_and = 360°
no

Polygon diagonals

Consider an n-sided polygon. To determine the number of diagonals (d), we use the following relationship:

d = n · (n - 3)
2

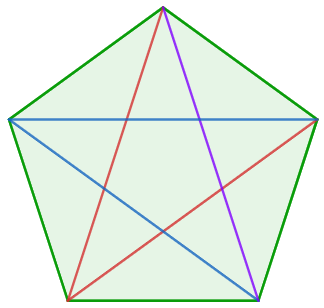
Example

Determine the number of diagonals in a pentagon and graph them.

We know that a pentagon has five sides, so n = 5. Substituting the expression, we have to:

d = 5 · (5 - 3)
2

d = 5 · 2
2

d = 5

Area and perimeter of polygons

O perimeter of polygons is defined by the sum from all sides. The area of ​​a polygon is calculated by dividing the polygon into figures that are easier to calculate the area, such as the triangle and the square.

THE_Δ = base · height
2

THE_square = base · height

Example

Determine a mathematical expression that represents the area of ​​a regular hexagon.

Solution:

Initially, consider a regular hexagon and all the straight line segments that connect the center of the polygon to each vertex. Thus:

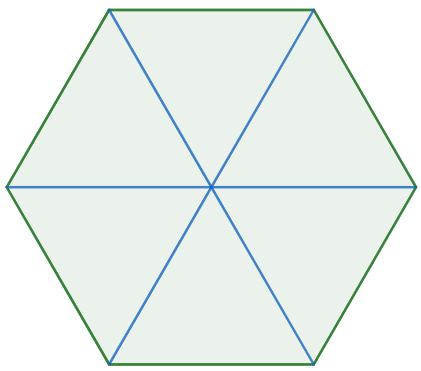
Note that due to the fact that the hexagon is regular, when dividing it, we find six triangles equilaterals, so the area of ​​the hexagon is six times the area of ​​the equilateral triangle, that is:

THE_hexagon = 6 · A_Δ

THE_hexagon = 6 · l² · √3
4

THE_hexagon = 3 · l² · √3
2

THE_hexagon = 3 · l²·√3
2

Read too:equilateral triangle area

solved exercises

question 1 – (Enem) A pool is shaped like a regular polygon whose internal angle is three and a half times the external angle. What is the sum of the interior angles of the polygon whose shape is the same as this pool?

a) 1800°

b) 1620th

c) 1440°

d) 1260°

e) 1080°

Solution

As we don't know the number of sides of the polygon, let's imagine just one of the vertices of this polygon.

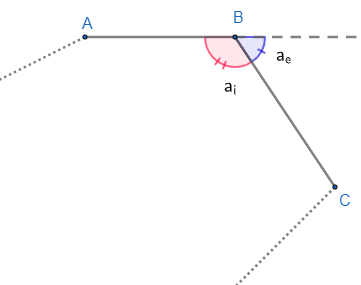
From the image we can see that:

The_i + the_and = 180° (I)

From the statement we have that:

The_i = 3.5 · a_and (II)

Substituting equation (II) into equation (I), we will have to:

3.5 · a_and + the_and = 180°

4,5 · a_and = 180°

The_and = 180°
4,5

The_and = 40°

However, we know that an interior angle is the division of 360° by the number of sides of the polygon. Thus:

The_and = 360°
no

40° = 360°
no

40n = 360°

n = 360°
40°

n = 9

Therefore, the sum of the pool's internal angles is:

s_i = (n - 2) · 180°

s_i = (9 - 2) · 180°

s_i = 7 · 180°

s_i = 1260°

by Robson Luiz
Maths teacher