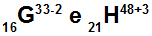real numbers it is the name given to the numerical set that is best known and used by everyone, as any integer or decimal number also belongs to that set. Its most used definition is as follows: The union between the set of rational numbers and the set of irrational numbers.
Some examples of real numbers:
1 - The set of natural numbers. Every natural number is also a real number, since natural numbers are also rational numbers.
2 – The set of whole numbers. Every whole number is also a real number, since whole numbers are also rational numbers.
3 – Decimal numbers. Every decimal number is also a real number, since decimal numbers belong either to the set of rational numbers or to the set of irrational numbers.
4 – Roots. Every root, square or not, is a rational or irrational number. Therefore, it belongs to the set of real numbers.
Real Number Properties
O set of real numbers has the following properties. Given the real numbers a, b and c:
1 - Commutativity: a + b = b + a
2 – Associativity: (a + b) + c = a + (b + c)
3 – Existence of neutral element of the sum: a + 0 = a
4 – Existence of an inverse element of the sum: a + (– a) = 0
5 – Commutativity: a·b = b·a
6 – Associativity: (a·b)·c = a·(b·c)
7 – Existence of a neutral element of multiplication: a·1 = a
8 – Existence of an inverse element of multiplication: a·(– a)= 1, where – a = 1/a
9 – Distributive property: a (b + c) = a·b + a·c
To understand the meaning of the definition "union between the set of rational and irrational numbers”, it is important to know the concept of union, as well as the elements belonging to each of these sets.
Union between sets:
The union is a case of operation between sets. Elements that belong to the union between two sets belong to a set or to another. The word or indicates that all elements of both sets belong to the union between them, but no elements are repeated in the union.
Do not stop now... There's more after the advertising ;)
For example: Let the sets A = {1, 2, 3} and B = {3, 4, 5}, the union between A and B is represented by AUB = {1, 2, 3, 4, 5} and designates the elements that belong to A or to B.
Set of rational numbers:
The set of rational numbers is formed by all numbers that can be written as a fraction. There are three types of numbers that fit this definition:
1 - whole numbers
2 – finite decimal numbers
3 – periodic tithes
This is because any whole number can be written as a fraction as long as the whole number itself is the numerator and 1 is the denominator. From this fraction, it is possible to find infinite fractions with the same result, simply multiplying numerator and denominator by the same number.
Finite decimals, on the other hand, can be transformed into fractions by completing the previous step and multiplying the fraction by some power of 10, where the exponent is equal to the number of decimal places of the decimal finite.
The periodic tithes, in turn, can be written as a fraction using a device that involves equations and systems of equations.
They are subsets of the rational number set: The set of natural numbers and the set of integers. Therefore, natural and integer numbers are also real numbers.
Set of irrational numbers:
The set of irrational numbers is complement thethe set of rationals. This means that irrational numbers are the set of numbers that are not rational. Thus, any number that cannot be written as a fraction is an irrational number.. The numbers that fit this definition are:
1 – non-periodic infinite decimals;
2 – inexact roots.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What are real numbers?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-numeros-reais.htm. Accessed on June 27, 2021.