THE Ellipse is a flat figure classified as a conical, because she can be obtained from the section of a plan in a cone. Finding a flat figure with an ellipse shape is quite common in everyday life. It has been widely studied to explain the movement of planets around the Sun, as the orbits of these stars are ellipses.
THE analytic geometry is the area of mathematics that seeks to describe algebraically geometric shapes, including, the ellipse is studied in depth in analytic geometry, being possible to describe it through an equation that takes into account its elements. The main elements of the ellipse are:
major axis
minor axis
focal distance
foci F1 and F2
We define the ellipse as the set of points where the sum of the distance of these points to the focus F1 and to focus F2 it is always constant.
Read too: What are the differences between flat and spatial figures?
What is an ellipse?
We know as an ellipse the flat figure formed by the section between the plane and the cone, in the following way:

To build the ellipse, it's need to know your two focuses, F1 and F2, and also the length of the major axis, which is the line that connects the ends of the ellipse, in the image below, represented by A1 THE2.
The length of the major axis is equal to 2a, so the ellipse is the curve formed by all points Pno where the sum of the distance from the point to the first focus (dPnoF1) with the distance from the point to the second focus (dPnoF2) is always constant and equal to 2a.
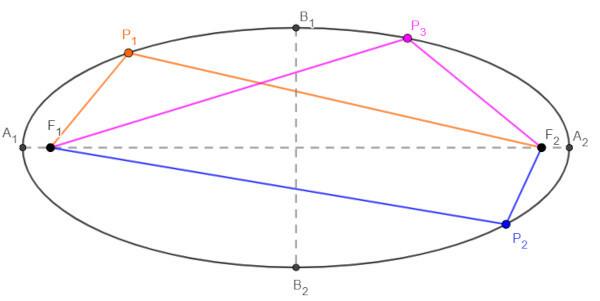
dP1F1 + dP1F2 = dP2F1 + P2F2 = dP3F1 + dP3F2 = dA1THE2 = 2nd
Do not stop now... There's more after the advertising ;)
Ellipse Elements
To fully understand the formation of the ellipse, it is necessary to know each of its elements. They are the foci, the center, the major axis and the minor axis. Based on them, it is possible to trace important relationships in the ellipse.

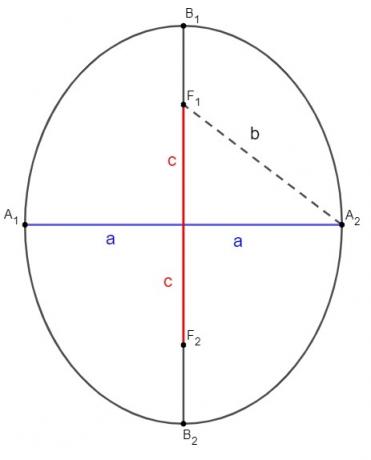
The center of the ellipse is represented by the point O.
Already the F points1 and F2 represent the ellipse foci.
the points A1 and the2 are ends of the horizontal axis of the ellipse, and points B1 and B2 are ends of its vertical axis.
The distance between B1 and B2 is equal to 2b (length of the ellipse on the minor axis).
The distance between A1 and the2 is equal to 2a (length of ellipse on major axis).
The focal length between F1 and F2 is equal to 2c.
Observation: It is important to realize that the F follow-up1B1 has a length equal to half of the horizontal axis, that is, dF1B1 = a. Thus, it is also possible to perceive an important Pythagorean relationship when analyzing triangle A1OB1. Note that he is a right triangle. Therefore, we can apply the Pythagorean theorem.
a² = b² + c²
There is another possibility for the ellipse, which is when the longest axis is the vertical axis. In this case, the elements remain the same.
In this case we can apply the Pythagorean theorem as well, getting as follows:
b² = a² + c²
Read too: What are the elements of a polygon?
Ellipse equation
The study of the ellipse analytically is done in the Cartesian plane. Analytical geometry seeks to describe, through equations, the figures of the plane geometry. Thus, it is possible to describe the figure through the so-called ellipse equation.
First, we will make examples of an ellipse whose foci are contained either on the x-axis or on the y-axis, that is, the origin of the ellipse coincides with the origin of the Cartesian plane.
In this case, there are two possibilities, when the major axis is the vertical axis and when the major axis is the horizontal axis:

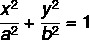
Observation: The foci are always contained in the longest axis, so if a > b, the foci are contained in the horizontal axis, and if b > a, they are contained in the vertical axis.
The center of the ellipse is not always at the origin of the Cartesian plane, which does not prevent the development and adaptation of the ellipse equation for this case. When the ellipse is offset from the origin O( x0, y0), its equation can be described by:
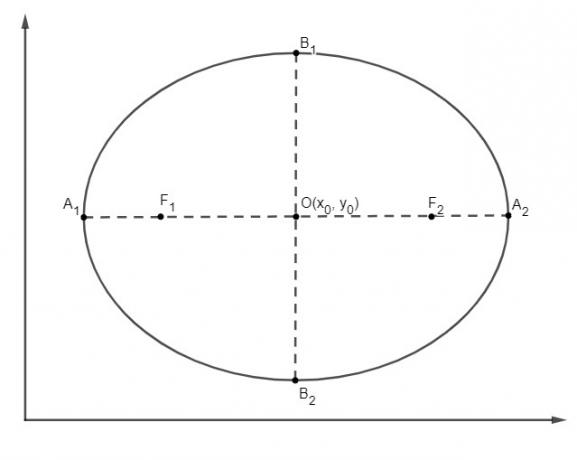
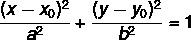
Read too: What is the reduced equation of the circumference?
Ellipse eccentricity
We know as eccentricity thereason between length c and half the length of the longest axis of the ellipse. Assuming the longest axis is horizontal, the eccentricity is calculated by:
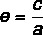
If the ellipse is on the vertical axis, the eccentricity will be calculated by:
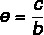
THE eccentricity tells us how flat the ellipse is, the larger the eccentricity value, the closer to a circle the ellipse will be. As the major axis always has a length greater than the focal length, so consequently c < a, so this division is always a number between 0 and 1.
ellipse area
As the ellipse has a rounded shape, to calculate its area, we use the constant π and also the measure of half the horizontal length and half the vertical length, so, We have to:
A = abπ
A: ellipse length
a: half the length of the horizontal axis
b: half the length of the vertical axis
Example:
Calculate the area of an ellipse, with the foci on the horizontal axis, whose longest axis measures 50 cm, and the shortest one 36 cm.
As the major axis is horizontal, then the foci are contained in it. Therefore, we have to:
2nd = 50
a = 50/2
a = 25
And on the vertical axis, we have to:
2b = 36
b = 36/2
b = 18
So the area of the ellipse is given by:
A = abπ
A = 25 · 18π
A = 450π cm²
solved exercises
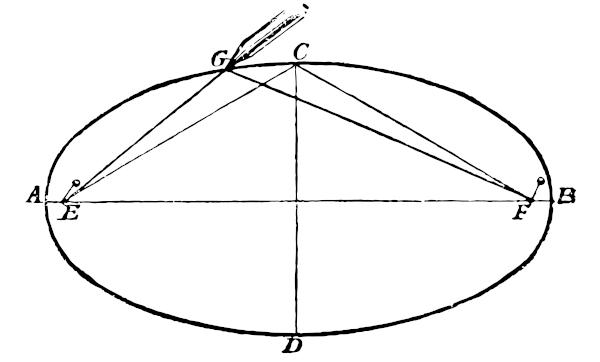
Question 1 - When analyzing the following ellipse, the alternative that contains its focal length is:

A) 5
B) 4√3
C) 4
D) 16
E) 8√3
Resolution
Alternative E.
The focal length is equal to 2c, and, in addition, a = 8 and b = 6. As the foci are contained on the x-axis, then we have to:
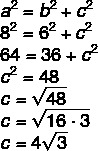
Since the focal length is equal to 2c, then 2c = 8√3.
Question 2 - (IFB) Considering an ellipse with center at the origin, foci on one of the coordinate axes and passing through points (5, 0) and (0, 13), determine the foci of the ellipse.
a) (13, 0) and (-13, 0)
b) (0, 13) and (0, -13)
c) (12, 0) and (-12, 0)
d) (0, 12) and (0, -12)
e) (5, 0) and (-5, 0)
Resolution
Alternative D
Note that it passes through point (0, 13), which indicates that b = 13, and also that it passes through point (5.0) a = 5. As b > a, we have to:
b² = a² + c²
13² = 5² + c²
169 = 25 + c²
169 – 25 = c²
144 = c²
c = √144
c = 12
Since b is larger, then the focus is on the vertical axis, ie (0, 12) and (0, -12).
By Raul Rodrigues de Oliveira
Maths teacher