O rectangle it is a polygon studied in plane geometry. As it has four sides, it is classified as a quadrilateral, and is called rectangle because it has the four right angles, that is, with a measure of 90º.
the rectangle has inherited properties for being a quadrilateral and also specific properties. To know the area of a rectangle, we calculate the product of the base and the height; its perimeter is equal to the sum of all its sides. The rectangle has two diagonals, and one of their properties is that they are congruent. To find the length of the diagonal, we apply the Pythagorean theorem.
Read too: Circle and circumference - geometric shapes with many features
Rectangle Elements

The rectangle is a polygon with four sides and whose angles are straight. That Geometric form it is quite common in everyday life, such as the floor plan of homes, the faces of boxes, doors, among other objects that have this shape.
The rectangle has four sides, four vertices, four internal angles, and it is possible to draw two diagonals.

- A, B, C and D are the vertices of the rectangle.
- AB, AD, BC and CD are the sides of the rectangle.
- AC and BD are diagonal.
Rectangle Properties
The rectangle has important properties, inherited by the fact that it is a parallelogram, that is, have parallel sides. We have to:
- Opposite sides are parallel and congruent.
- Two internal angles on the same side are always supplementary, that is, they add up to 180º.
- All angles measure 90º, so, as with other parallelograms, opposite angles are congruent and adjacent angles are always supplementary.
- The diagonals are always congruent.
- The meeting point of the diagonals is also the midpoint of each of the diagonals.
See too: Point, Line, Plane and Space: Basic Concepts of Geometry
rectangle area
The rectangle area calculation is quite recurrent to find the area of other polygons. Because it has a very simple formula for calculating area, it is common to divide a polygon into multiple rectangles to calculate its area, and therefore the rectangle area is one of the most important among the polygons.
To know the area of the rectangle, we calculate the multiplication between base and height:

A = b × h
rectangle perimeter
The perimeter of the rectangle, as in the other polygons, is equal to the sum of all its sides.
Calculating the perimeter is finding the length of the polygon outline. In the rectangle, as we know, the sides are congruent two by two, it is then possible to calculate the perimeter of the rectangle using the formula:
P = 2(b + h)
Example:
Calculate the perimeter and area of the rectangle that has sides measuring 5 cm and 7 cm.
Such as addition is commutative, that is, the order of the portions does not change the sum, we can choose b = 5 and h = 7.
P = 2(5 + 7)
P = 2 · 12
P = 24 cm
A = b × h
A = 5 × 7
H = 35 cm²
Rectangle Diagonal
When we draw any of the rectangle's diagonals, we're dividing it into two right triangles, so, you can find the diagonal length of the rectangle by pit's theoremánow.

d² = b² + h²
rectangle trapeze
The trapeze, like the rectangle, is a quadrilateral. The difference is that, in the trapeze, only two sides are parallel, and the other two are not. When a trapeze has two of its right angles, he is known as trapeze rectangle.
rectangle triangle
O right triangle it is a polygon of great importance for mathematics. Study in depth, it is where most of the studies of the trigonometry, and there is also the important Pythagorean relationship between its sides. rectangles, squares and diamonds can always be divided, by their diagonals, into right-angled triangles. A triangle is a rectangle when it has one of its right angles, that is, equal to 90º.
Also access: What are the criteria for classifying a triangle?
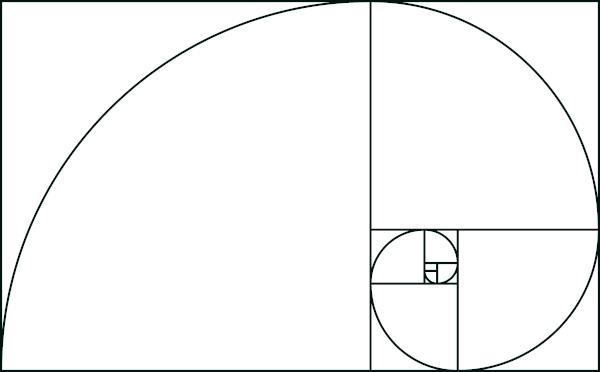
golden rectangle
The golden rectangle, also known as the golden rectangle, is much admired by mathematicians, architects and artists. He is thus known for having the golden ratio.. Realizing the existence of the golden proportion in paintings and artistic constructions is quite common. Many times this proportion it is related to objects considered beautiful, because of the harmony it preserves. When we divide the rectangle, for it to be considered golden, we have to:
solved exercises
Question 1 - (IFG 2019) Consider that the size of a television, given in inches, corresponds to the length of your diagonal and that, in the case of full-size televisions, the width and height follow, in an orderly fashion, the 4:3. Look at the figure below and assume that 1 inch is approximately 2.5 cm
Regarding a 40-inch flat-panel television, it is correct to state that its width and height are, respectively:

A) 60 cm and 45 cm
B) 80 cm and 60 cm
C) 64 cm and 48 cm
D) 68 cm and 51 cm
Resolution
Alternative B. By tracing the diagonal of the figure, we know that it is possible to form a right triangle. As the sides have a 3-to-4 ratio, then we have the height to measure 3x, and the length to be 4x. Applying the Pythagorean theorem, we have to:
(3x) ² + (4x²) = 40²
9x² + 16x² = 1600
25x² = 1600
x² = 1600/25
x² = 64
x = √64
x = 8
Knowing the value of x, then one side measures, in inches:
3x → 3 · 8 = 24"
4x → 4 · 8 = 32"
Since 1 inch equals 2.5 cm, so we have to:
24 · 2.5 = 60 cm
32 · 2.5 = 80 cm
Question 2 - In a rectangle, one side is equal to 2/3 of the other side. Knowing that its perimeter is equal to 120 cm, the area of this rectangle is:
A) 326 cm²
B) 532 cm²
C) 432 cm²
D) 864 cm²
Resolution
Alternative D

By Raul Rodrigues de Oliveira
Maths teacher

