To understand the electrical potential of an electrified conducting sphere, we must first analyze what happens inside the sphere, which when The electrified battery quickly reaches electrostatic equilibrium due to the uniform spread of excess charges across its surface. external. In this situation, the electric field and the electric force within that sphere are null.

The electric field (E) inside the electrified sphere is null
Thus, if we place an electrified particle with charge q on a point A inside the sphere and it is displaced to a point B, also internal to the sphere, no work (τ) will be performed on it and by the equation: VTHE – VB = τ/q, we have to VTHE = VB, if youTHE were different from VB there would be charge flow between these two points, and this cannot occur when the sphere is in electrostatic equilibrium, thus, we can say that:
Inside an electrified sphere in electrostatic equilibrium, all points have the same electrical potential.
When we have a point S exactly on the surface of the sphere, it happens again that the work done to carry a charge q from A or B to S is equal to zero, thus we can conclude that:
The electrical potential at any point within an electrified sphere in electrostatic equilibrium is equal to the potential at its surface.
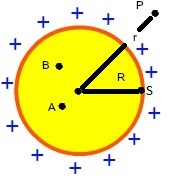
The sphere can be considered as a point charge
Now we have to know what is the value of the electric potential on the surface of the sphere in electrostatic equilibrium, and for that we must remember that spheres are electrified under these conditions of electrostatic equilibrium can be thought of as having all its charge concentrated at its center, so if we have a sphere of radius R, the potential on its surface will be given by V = KOQ/R, and also if we have a point P located outside the sphere at a distance r from its center (thus r > R), the electric potential of the sphere in P can be calculated by the equation (see figure above):
V = KOQ/r
The potential for points inside the sphere (r ≤ R) is constant, and for points outside the sphere (r > R) it decreases inversely proportional to the distance (r).
By Paulo Silva
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/potencial-eletrico-uma-esfera-condutora-eletrizada.htm
