THE division is one of the four basic operations of the math and it's inverse to multiplication. The division of a number consists of its fractionation, in your fragmentation, which can result in a integer or a decimal number.
As with the other fundamental operations of mathematics, division is also very present in our daily lives, therefore, it is essential to know this process well, in order to acquire practice and make this calculation more agile.

Division elements
when are we going to split a number P by a number d, we must get a number what that multiplied by d be equal to P. Each of these elements is given a name: P is called dividend, of the divider and what the quotient.
It is not always possible to find this number what, in some cases, the multiplication of d per what just is very close to P. In these situations, the difference of P by the result of the multiplication of d per what it's called rest and will be denoted by r.
Do not stop now... There's more after the advertising ;)
→ Examples
a) 28: 2 = 14, since 2 ·14 = 28 → Exact division
b) 29: 2 ≠ 14, since 2 ·14 = 28 → Inexact division, has remainder = 1
When the rest doesn't show up, that is, when r = 0, we say that the number P is divisible by d. Otherwise, P is not divisible by d.
We can say that:
P = d ·q + r
Now let's look at a method that makes it easy to find all these elements: key method. See the figure below:

→ Example
In dividing the number 25 by 5 we have:

Number 25 is the dividend, number 5 is the divisor, 5 is the quotient, and zero is the rest of dayeyesight. Note that to perform the division it is necessary to find a number that multiplied by 5 is equal to 25, in this case, the number is 5.
See also that we can write the number 25 as follows:
25 = 5 · 5 + 0
See too: d criteriaivisibility: rules that help the calculation of division
Division step by step
To facilitate the division process, we have an algorithm, that is, we have a step by step that can facilitate. To verify this process, let's take the following division 64: 4.
First step: mount the operation using the key method.

Second step: try to find a number that multiplied by 4 equals 64. As this is not an easy task, let's take only the number 6 to divide with the number 4, that is, the tenth digit. Thus, we must determine an integer that multiplied by 4 equals 6 or comes as close as possible. Look:
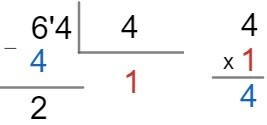
Third step: continue the division by descending the unit digit, which was not divided, in this case, the 4. Look:

The process comes to an end when we get the remainder equal to 0. Otherwise, we must continue the division following the same procedures.
Read too: Tips and tricks for division calculations
Signal game in division
At whole number division, we must be aware of the signs. We must remember the properties of integers:
first number sign |
second number sign |
result sign |
+ |
+ |
+ |
+ |
- |
- |
- |
+ |
- |
- |
- |
+ |
→ Examples
a) (+ 55): (+11) = +5
b) (+243): (– 3) = – 81
c) (– 1050): (+5) = – 210
d) (– 12): (– 6) = +2
Comma division
In the division, there are two situations where the comma can appear: the first is when the quotient is not an integer, and the second is when the dividend and divisor are not integers. Let's see how to solve each of these cases through examples.
Division where the quotient is not integer
This case occurs when the numbers are not divisible, that is, the remainder of the division is a non-zero number. To carry out the division, we must follow the same step-by-step mentioned above.
However, when the remainder is a number that can no longer be divided, we must add a comma in quotient it is a zero in the rest of the units.
Look:
The division between the number 55 and 2 is not exact, as 55 is not even, so let's perform the division and find the result by following the step.

Note that the remainder of the division is nonzero and you cannot divide it by the quotient. The second step is to add a comma to the quotient and a zero to the remainder in the unit place.
Then:
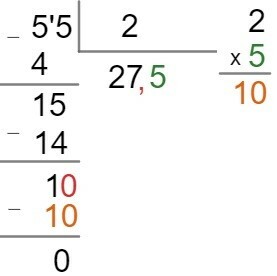
Note that after adding the comma and the number zero, the division operation followed the step by step again.
Division where the dividend and divisor are not integers
First step: eliminate the comma from the dividend and the divisor.
For this to occur, the same number of decimal places must be moved in both the divisor and the dividend. This is allowed, as the division is nothing more than a fraction where the dividend is the numerator and the divisor is the denominator. That way we can multiply the dividend and the divisor by potencies of10, which is the equivalent of walking to decimal places.
Second step: follow the step by step presented above.
→ Example
Let's divide the number 0.05 by 0.2 following the step by step.

We must go 2 decimal places so that the comma disappears from the dividend, so we must also go 2 decimal places on the divisor, that is, we are going to multiply the divisor and the dividend by 100.
0,05 ·100 = 5
0,2 ·100 = 20
Now the division is:

To start doing the division, we must find a number that multiplied by 20 equals 5, but that whole number doesn't exist! Then we add 0 and a comma to the quotient, 0 to the dividend, and we proceed with the division normally.
Reminder:after the process of putting the comma in the quotient, we can put the number 0 in the unit place whenever necessary.

Read too: Division with fractions: learn how to calculate
Exercise solved
question 1 – João is going on a trip of 521 kilometers. To make the trip more secure, he decided to take it in two stages. How many kilometers will John travel per day?
Solution
The total trip is 521 kilometers and will be done in 2 days, to determine the amount of kilometers that will be covered per day, we must divide these numbers.

Therefore, John will travel 260.5 kilometers a day.
By L.do Robson Luiz
Maths teacher

