Let's consider a body on a flat, horizontal surface, as shown in the figure above. Suppose this body has mass m and speed 
. After a certain moment, a force resulting from intensity will act on this body. 
constant and parallel to the initial velocity. Keeping the initial conditions, at any moment the body starts to have a speed 
and will have traveled a distance 
.
We can determine the work done by the resulting force 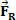constant, along the displacement , this way:
According to the fundamental principle of dynamics (Newton's Second Law), in module:
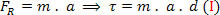
Torricelli's equation can be rewritten as follows:
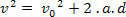
Do not stop now... There's more after the advertising ;)
Substituting equation (II) into equation (I), one finally obtains
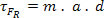
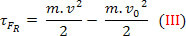
the scalar physical greatness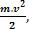 
that appears in this development, came from work and is linked to the movement. It was, therefore, called kinetic energy. We can define it as follows:
- a body of mass m endowed with instantaneous velocity v, for a certain reference, has a kinetic energy ANDç, given by:
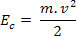
The equation (III) that we obtained earlier is called Kinetic Energy Theorem. We can state this theorem as follows:
- the work of the resultant force acting on a body in any given time interval is equal to the variation of its kinetic energy in that time interval. So we can write:
By Domitiano Marques
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
SILVA, Domitiano Correa Marques da. "Resultant force work: movement energy"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/trabalho-forca-resultante-energia-movimento.htm. Accessed on June 27, 2021.
