THE square root is a kind of mathematical operation, just like addition, multiplication, and others. She is the reverse operation of potêanceof two, that is, calculate the square root of a numberThe is to look for the number raised to 2 that results in The.
Also, this root can be exact or not. When it is exact, the number is called a perfect square. In geometry, it is useful for determining the side of squares.
Read too: Potentiation and radiciation of fractions – how to solve it?
Radiation
At square root, the index of the root is 2. It is the most common among radiciations, but it is also possible to calculate cubic root, fourth root, among other roots.
Radiciation is the inverse of potentiation. For example, if I ask for the fifth root of a number no, we're looking for the number that, multiplied by it 5 times, gives no.
Elements of Radiation
The operation is represented by:

 radical
radical
n→ index
a→ rooting
b→ root
As we are going to study the square root, the index will always be equal to 2. In a radiciation, when the index is 2, we don't need to write it.

Calculating the square root
Calculating the square root can be done from the head through times tables when we know the root. When the number is very large, an alternative is factor this number. Calculate the square root of The is to find the number B that when we multiply b.b, results in The.
Examples
Square Root Types
A square root can be exact or not. For us to be able to classify, we need to take into account whether the answer is a rational number or a number irrational.
exact square root
A square root is exact when it results in a rational number, as a fraction, a whole number, a decimal number, as long as, by multiplying this number by itself, we find exactly the root.
Examples
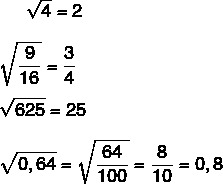
When the number for which we want to calculate the exact square root is very large, it is ideal to resort to factoring that number. Since we are calculating the square root, let's group this factorization as powers of two as shown in the following example.
Example
Find the square root of 3600.

Now that we've done the factorization, let's calculate the root of 3600 in factored form.
We can see that the root of a squared number is equal to the number itself. For example, we know that 3 squared is 9 and that the root of 9 is equal to 3. So we can simplify exponent 2 with the radical.

In the exact root, when the answer is a natural number, it is known as a perfect square. See all perfect squares from 0 to 100.
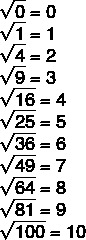
The perfect squares from 0 to 100 are 0, 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100.
not exact square root
There are cases where the root is not exact. When this happens, we can find the best possible approximation to the root of this number, since the answer is an irrational number. For this approximation, let's use the perfect squares we already know.
Example
To find the root of 40, let's compare it to the exact roots we know. Looking at the perfect squares, we know that 40 is between 36 and 49.
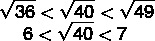
Now let's find the decimal number between 6 and 7 that is closest to 40.
6,1² = 37,21
6,2²= 38,44
6,3²=39,69
6.4²=40.96 → passed 40, so let's use the previous decimal number for the approximation.
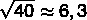
Note that 6.3² isn't exactly 40, but it's close, so this square root isn't exact.
See too: Root calculus - ways to solve
Geometric interpretation of square root
Some math history books say the square root arose for solve problems of areas of square. Suppose we want to find the side of a piece of land that is shaped like a square and its area is equal to 169 m².

Such as square area is calculated by l², so to calculate the root of 169, geometrically, is to find the side of the square that has that area.
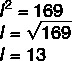
The square side is 13 meters.

solved exercises
Question 1 - What's the best approximation for the square root of 72?
A) 8.1
B) 8.2
C) 8.3
D) 8.4
E) 8.5
Resolution
Alternative D.
We know that 72 is between the perfect squares 64 and 81, so we have to:
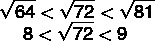
8,1²= 65,61
8,2²= 67,24
8,3²= 68,89
8,4²= 70,56
8.5²= 72.25 → passed, so the best approximation is the previous one, 8.4.
Question 2 - Which of the roots below is not exact?

Resolution
Alternative C.
a) It has an exact root equal to 11, since 11² =121.
b) It has an exact root equal to 1.3, since 1.3² = 1.69.
c) Does not have exact root
d) It has an exact root, as the numerator 1²=1 and the denominator 2²=4, so the root of this fraction is equal to ½.
e) It has an exact root equal to 1.



