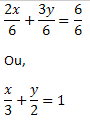THE rule of three compound is a method used to find unknown values when the problem involves quantities that have proportion. It is important to remember that there are two possibilities for quantities when they are proportional. They can be directly or inversely proportional.
When there are three or more quantities that are proportional, we apply the compound rule of three following a step-by-step solution. The steps are:
identification of quantities;
table construction;
analysis of the relationship between the quantities; and
solving the equation generated by the problem.
The rule of three compound is an extension of the rule of three simple, so to master the compound it is essential to master the simple resolution, which is applied when there are only two quantities.
Read too: Percentage calculation with rule of three
Step by step to solve a compound rule of three

To solve problems involving compound rule of three, we need to follow a few steps. These steps are the same regardless of the quantity of quantities involved in the problem.
1st step: identification of quantities and construction of the table.
2nd step: theanalyze the proportion that exists between the quantity that contains the unknown.
3rd step: reverse the reason if there is any inversely proportional magnitude to the magnitude that contains the unknown; if not, go straight to step four.
4th step: ride the equation, leaving the magnitude that has an unknown in the first member of the equality and calculating the product among the others, which will remain in the second member.
→ Rule of three composed with three magnitudes
Example:
A construction company was hired to carry out the renovation of all schools in the municipality of Cocalzinho, in Goiás. Schools are built with standard shape and size in this city, so the outer wall is the same size. Knowing that 4 painters would take 8 days to paint 6 schools, how long would it take 8 painters to paint 18 schools?
Resolution:
The quantities are: number of painters, days and number of painted schools.
Now let's build the table, always starting with the magnitude of the unknown:

Now it is necessary to analyze the relationship that exists between the quantities. In the rule of three compound, the comparison is made to from the magnitude of the unknown in relation to the others, that is, let's compare days and painters and days and schools.
To compare days and painters, let's fix the number of schools. In the same number of schools, if I increase the number of painters, the number of days it takes me to renovate decreases, so these quantities are inversely proportional.

Comparing days and schools and fixing the number of painters, when analyzing the proportionality, if the number of schools increases, the number of days also increases.

In short, we have that days is inversely proportional to the number of painters and directly proportional to the number of schools.
To build the equation, it is necessary to isolate the fraction of the unknown and invert the fraction of the quantity inversely.

See too: Three Most Mistakes Made Using the Rule of Three
→ Rule of three composed with four magnitudes
To solve three-rule compound problems with four magnitudes, we follow the same steps presented above.
Example:
In a truck parts factory, to produce a certain part, we know that 3 machines, working for 5 days, connected for 4 hours, they manage to produce 4,000 pieces, which is the monthly demand from factory. During the process, one of the machines broke down, which made the factory decide to increase the number of days of production to 6 days, and the working time of the machines to 8 hours. How many parts will be produced in this situation?
Resolution:
The quantities are: number of machines, days, hours and number of parts.
Analyzing the proportions between the quantities, comparing machines with parts, days with parts and hours with parts, we can say:
Do not stop now... There's more after the advertising ;)
if I increase the number of machines, consequently the production of parts will increase;
if I increase the number of working days of the machines or even hours of work, there is also an increase in the quantity of parts produced, therefore, all quantities are directly proportional to the quantity of parts produced.
Assembling the table, we have to:

Now solving the equation:
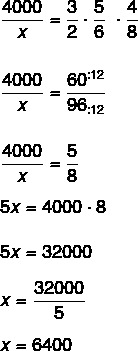
Difference between simple and compound rule of three
Working with quantities is quite common in our daily lives and, when the quantities are direct or inversely proportional, it is possible to predict what will happen to a quantity by comparing between them.
THEsimple rule of three is used for problems with only two magnitudes.. It is applied when we know three values, two of one magnitude and one of another. The compound rule of three is applied in slightly more complex situations, involving more than two quantities.
It is noteworthy that the methods are very similar, as the compound rule of three is nothing more than an extension of the simple rule of three.
Also access: Three Basic Mathematics Concepts for Enem
solved exercises
Question 1 - (Enem 2013) An industry has a water reservoir with a capacity of 900 m³. When there is a need to clean the reservoir, all the water needs to be drained. The drainage of water is done by six drains, and lasts 6 hours when the reservoir is full. This industry will build a new reservoir, with a capacity of 500 m³, whose water flow should be carried out in 4 hours, when the reservoir is full. The drains used in the new reservoir must be identical to the existing ones.
The number of drains in the new reservoir should be equal to:
A) 2
B) 4
C) 5
D) 8
E) 9
Resolution
Alternative C.
The grids are: capacity, number of drains and time in hours. The quantity that contains the unknown value is the number of drains, so let's compare it with capacity and time.
Fixing the time, if I increase the amount of drains, the capacity to drain water will also increase, so these quantities are directly proportional. If I increase the amount of drains, fixing the volume, the time it takes to drain all the water will decrease, so drains and time are inversely proportional.
Assembling the table, we have to:

Inverting the fraction and the ratio of hours, we have to:
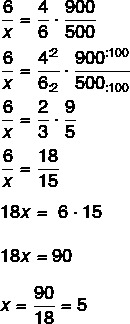
Question 2 - (Enem 2015 – second application) One confection had 36 employees, reaching a productivity of 5,400 shirts per day, with a daily workday for employees of 6 hours. However, with the launch of the new collection and a new marketing campaign, the number of orders rose sharply, increasing daily demand to 21,600 shirts. Seeking to meet this new demand, the company increased its workforce to 96. Still, the workload needs to be adjusted.
What should the new daily working hours of employees be for the company to be able to meet the demand?
A) 1 hour and 30 minutes.
B) 2 hours and 15 minutes.
C) 9 hours.
D)16 hours.
E) 24 hours
Resolution
Alternative C.
The quantities are: number of employees, number of shirts and time in hours per day. The unknown is in the magnitude hours a day, so let's analyze its proportion with the other magnitudes:
setting the number of shirts, if I increase the number of employees, the working time per day decreases, so employees and hours are inversely proportional;
Fixing the number of employees, if I decrease the hours worked per day, consequently the number of shirts will decrease, so these quantities are directly proportional.

Assembling the reasons and inverting the employees' reason, we have to:

By Raul Rodrigues de Oliveira
Maths teacher