Probability is a field of mathematics that studies the chances of an event occurring in a random experiment. Probability can be used to calculate the odds of a given result on the roll of a die or even the odds of someone winning the lottery.
Mathematical probability is represented by the set of numbers between 0 and 1:
- When an event has probability 0, its occurrence is impossible,
- When the probability of an event is 1, that event will happen for sure.
How to calculate probability?
To calculate probability, divide the number of expected event occurrences by the total number of events in a random experiment. For example, if we wanted to calculate the probability that a coin tossed on the ground would fall with the "crown" face up, we would have:
- One (1) possibility of occurrence of the event we want: "crown",
- Two (2) total event possibilities: "heads" and "tails".
So we split 1/2 and we have a "tails" probability of 1/2 or 50%.
probability formula
To better understand how to calculate probability, look at the formula:
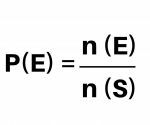
Where:
- P(E) = probability of occurrence of an event AND
- n (E) = total number of occurrence of event E
- n (S) = number of occurrences of the sample space S
Before looking at practical examples of calculations, understand some fundamental concepts of probability:
random experiment
The probability can only be calculated in cases of random experiments, that is, in situations where it is not possible to determine or predict the outcome..
One example of a random experiment is rolling a die. If the die is not hooked (with more weight on one of the faces, for example), it is not possible to determine which face will fall face up, ie, the result of the roll depends on chance.
Another example would be a bag filled with blue and yellow balls of the same size and weight. By choosing one of the balls at random, without seeing them, there is no way of knowing whether a blue or yellow ball will come out, so this experiment is random.
Sample space
The sample space is the set of all possible outcomes in a random experiment. For example, when we roll a die, the sample space (S) is represented by all the values of the die, that is: (S) = {1,2,3,4,5,6}.
The sample space, then, is the set of all the faces of the die, as the 6 faces are the 6 possibilities of happening after a roll. Thus, although it is not possible to predict the result, we know that it will be within the sample space.
Event
Event (E) is a subset of the sample space (S). When rolling a die, the occurrence of the number 5, E = {5}, or an even number, E = {2,4,6}, can be determined as an event.
Types of events
Right event: a certain event is one that represents the sample space itself (E = S) and it will happen with certainty. After the roll of a standard die (with numbers from 1 to 6), the chance of rolling a natural number is 100%, as all numbers from 1 to 6 are natural.
Impossible Event: an impossible event is one that has a 0% chance of happening. When rolling a standard die, the chance of rolling the number 8 is zero, as the die has no face with the number 8.
Complementary events: complementary events are those in which the intersection between the events is represented by an empty set and the union is represented by the entire sample set.
The probability of occurrence of a even number and from one odd number when throwing a die, they are complementary events, as the sum of the occurrences of these two events is represented by the 6 possibilities: E = {1,2,3,4,5,6}.
In this case there will be no intersection, as a number cannot be even and odd at the same time.

Probability Exercises
Let's exercise using the probability formula with an example:
- When rolling a die, what is the probability of the occurrence of the following events:
a) Odd number:
There are three possibilities to get an odd number: E = {1,3,5}. In this case, n (E) = 3. If the total number of possibilities n (S) = 6, we have:
P(E) = 3/6
P(E) = 1/2 or 50%
In that case, there is a 50% chance that an odd number will come out.
b) Number 5:
There is only one possibility to get the number 5, so n (E) = 1. Considering the total number of possibilities n (S) = 6, we have:
P(E) = 1/6
P(E) = 0.166 or 16.6%
In this case, there is a 16% chance that the number 5 will be rolled when rolling a die.
Note that, as we said at the beginning of the text, the probability will always be a number between 0 and 1, where 1 represents a 100% chance of the occurrence of an event and 0, the impossibility of occurrence of the event.
See also the meaning of arithmetic, percentage and geometry.

