Cartesian plane, also called orthogonal Cartesian system or coordinate plane, is a coordinate system consisting of two perpendicular axes. This means that, at the point where these two lines intersect (intersection point), a 90° angle (right angle) is formed. The horizontal axis is called the abscissa (x) axis. The vertical is called the ordinate (y) axis.

This mathematical tool is so named because its inventor was the French philosopher and mathematician. Rene Descartes (1596-1650). Used to determine the position of a point in space, the orthogonal system is super important in disciplines such as geometry and geography, in addition to having many uses in daily life.
Cartesian plan elements

ordinate axis
Identified with the letter y, the ordinate axis is the vertical straight of the Cartesian plane. If we look closely, we will see that both axes are numerical scales. Above point 0, numbers on this scale are positive. Down, negatives.
abscissa axis
Identified with the letter x, the axis of the abscissa is the
horizontal straight of the Cartesian plane. To the right, numbers on the numerical scale are positive. To the left, negatives.See too: Definition of Axis
Point 0
Also called origin, it is the exact point where the two lines meet, forming a right angle. Above the 0 point, numbers are positive. Down, negatives. On the right, positives. On the left, negatives.
quadrants
Another important element of the Cartesian plan is the quadrants. Notice how the two lines that intersect at point 0 produce an image divided into four segments. Each of these segments is called a quadrant. Any point on the plane will fall within any of these four quadrants.
What are the coordinates of the Cartesian plane?
Coordinates are the numbers that, together, give the exact location of a point on the Cartesian plane.
Have you ever played naval battle? The logic is exactly the same. To fire a shot at enemy ships, you need to say what the coordinates are. In other words: what are the values on the vertical and horizontal axes that indicate the target of your cannon.
Thus, each point on the plane is determined from a pair of pieces of information. give the name of ordered pair to this set consisting of two real numbers that represent values on the two axes and give us the exact location of a point on the plane. The first value of the pair is the abscissa (x). The second, the ordinate (y).
any point in quadrant 1 (Q1) will have positive coordinates (+,+). O quadrant 2 (Q2) is formed by points where the x coordinate is positive and y is negative (-,+). O third quadrant (Q3) it consists of points formed by negative coordinates (-,-). already the fourth quadrant (Q4) has the x coordinate positive and y negative (+,-).
Examples
Example 1
Suppose you want to know the coordinates of four points on the Cartesian plane. Suppose the points are these:

How can I find the coordinates of these points? Just draw two lines: one of them vertical, starting from the point until finding the x axis; another horizontal, starting from the point until finding the y axis.

Example 2
It is also possible to find the location of a point on the Cartesian plane from the coordinates. Just draw two lines - one starting from the x-axis, the other from the y-axis. The meeting between the two lines is the point.
We have the following ordered pairs: (3,4), (-4.1), (-3,-3) and (2,-3). These pairs determine points on the Cartesian plane. But what is the exact location of these points?
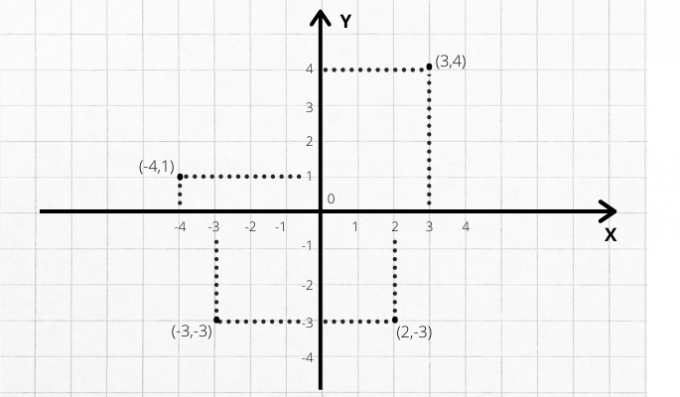
Note that each of them is located within one of the four quadrants. In Q1, we have (3,4); that is, coordinate 3 on the abscissa axis (x) and coordinate 4 on the ordinate axis (y). In Q2, we have (-4.1). In Q3, (-3,-3). In Q4, (2,-3).
What is the Cartesian plan for?
The Cartesian plane serves as a reference system so that points can be located in the plane or in space.
The Cartesian plane is very useful in graphing solutions to equations that contain two variables.
Second-degree functions can also be represented geometrically in the Cartesian plane - in this case, the geometric figure is the parabola. First-degree functions are represented by straight lines in the Cartesian plane.
At practical life, the Cartesian plan is also very useful. For its ability to provide a representation of space, the Cartesian system is fundamental, for example, in architecture and civil construction, as it is used as a basis for the preparation of house plans and buildings.
O GPS system, widely used today in navigation, aviation and even in the daily movements of individuals, is based on the Cartesian coordinate system. From any point (user), it is possible to determine its geographic coordinates (latitude, longitude and altitude) in a three-dimensional Cartesian system (x, y, z). This requires satellites and a ground station.
See too:
- Definition of Cartesian
- Definition of Geometry
- Meaning of Perpendicular