We've put together for you some examples of solved exercises on the movement uniform to improve your understanding of the topic. O movementuniform occurs when a mobile moves along a trajectory straight and with velocityconstant, without acceleration.
When a piece of furniture moves in uniform motion, it travels through spaces for equal intervals of time. Also, in uniform motion, the average speed is equal to the instantaneous speed.
In uniform motion, we can calculate the speed at which a body moves using the equation shown below:

v - average speed
S – displacement
t - time interval
Want to know more details about uniform motion? Check out our article that presents all the theory behind this type of movement: Uniform Movement.
See too: How to solve Kinematics exercises?
solved exercises
1) A vehicle moves with a constant speed of 36 km/h. Next to it, another vehicle travels at a constant speed of 54 km/h. Check the alternative that indicates the distance, in km, between these vehicles after a time interval of 5 minutes.
a) 5.0 km
b) 2.0 km
c) 1.5 km
d) 3.0 km
e) 18 km
Template: Letter C.
Solving this exercise requires us to calculate the space traveled by the two vehicles, so that we can then find out what was the difference in the space covered by them. However, in this exercise, there are some units of measure for speed and time that require attention. Therefore, we transform the speeds, given in km/h into m/s, dividing them by a factor of 3.6. Then, it is necessary to multiply the time of 60 minutes by 60, in order to use the time informed in seconds. Note the resolution:

2) One person climbs an escalator with a base of 8 m and a height of 6 m at a constant speed of 0.5 m/s. Determine the amount of time needed for her to reach the top of this ladder.
a) 15 s
b) 20 s
c) 10 s
d) 40 s
e) 12 s
Template: Letter B.
To calculate the required ascent time, we need to use the formula for average speed. However, the displacement suffered while the person climbs the stairs occurs in the direction of the hypotenuse of a triangle whose legs are 8 m and 6 m and, therefore, we need to calculate it using the Pythagoras theorem, see resolution:
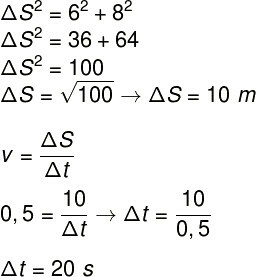
3) You want to travel 90 km away with an average speed of 60 km/h. A vehicle travels the first 30 km of this route in a time interval of 30 minutes (0.5 h). Check the alternative that shows the time remaining for the driver to complete the route so that he maintains the desired average speed.
a) 3.0 h
b) 2.0 h
c) 0.5 h
d) 1.0 h
e) 0.25 h
Template: Letter D.
As stated in the exercise statement, we want the average speed of the entire route to be 60 km/h. To do so, let's determine how long this trip should take place:

As the driver spends 30 minutes on the first 30 km of the journey and the total travel time cannot exceed 1.5 h, then the time left to cover the next 60 km is 1 h.
4) A train needs to complete a 400 km journey in a maximum time of 4 hours, moving at 80 km/h. After 30 minutes of travel, the train breaks down and is stopped for 30 minutes. Determine the average speed the train will need to develop for the rest of the journey to reach its destination on time.
a) 100 km/h
b) 120 km/h
c) 160 km/h
d) 90 km/h
e) 70 km/h
Template: Letter B.
To solve this exercise, we need to find out how far the train went before it broke down. According to the exercise, the train was moving at 80 km/h and, after 30 minutes, it broke down. Making the calculation, we found that this train traveled a distance of 40 km. As the repair of the train took another 30 minutes, there are only 3 hours left of the total journey time, so that the train is not late, and a distance of 360 km. In this way, we calculate the speed for the distance and the time remaining, then we find the value of 120 km/h. See the calculation:

By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/exercicios-resolvidos-sobre-movimento-uniforme.htm

