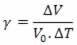We know that the orbits of the planets are elliptical, however, for the deduction of Kepler's Third Law, let's consider a circular orbit. Although the following demonstration is based on circular orbits, the results are also valid for elliptical orbits.
In the figure we have a planet orbiting the Sun. The centripetal force (Fc) is a gravitational force of attraction exerted by the Sun. The attraction forces exerted between planets and satellites are neglected, this is due to the fact that their masses are much smaller than the mass of the Sun.
Like the planet of mass (m) orbits around the Sun, in a circular motion and with angular velocity ( ), the resulting force on the planet, called centripetal force (Fc), is given by:
Fç=mω2 r
On what:
Fç:centripetal force;
m: mass of the planet;
ω: angular velocity of the planet;
r: radius of the planet's orbit.
Angular velocity is given by:
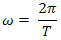
On what:
T: period of revolution on the planet.
Substituting equation 2 into equation 1, we have:
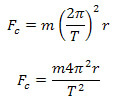
Note that the centripetal force is the gravitational force of attraction between the Sun and the planet. Thus, considering the Sun's mass as (M) and the planet's orbit radius as (r), which is the distance between the Sun and the Planet, the Law of Universal Gravitation can be written as follows:
Do not stop now... There's more after the advertising ;)
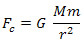
On what:
Equating equation 3 with 4, we will have:
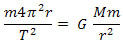
Soon:
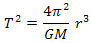
Look at equation 5 and note that the term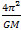 
is constant, as the unknowns refer to the universal constant and the mass of the sun, so the equation can be rewritten as follows:
T2=kr3
On what:
k: proportionality constant.
Equation 6 tells us that the square of a planet's period of revolution around the Sun is directly proportional to the cube of the distance between them.
By the equation above we can draw the conclusion that the farther the planet is from the Sun, the longer its period of revolution.
Kepler's Third Law, which we have just deduced, is also valid in relation to the Earth for the motion of the Moon and artificial satellites.
By Nathan Augusto
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
FERREIRA, Nathan Augusto. "Deduction of Kepler's Third Law"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/deducao-terceira-lei-kepler.htm. Accessed on June 27, 2021.
