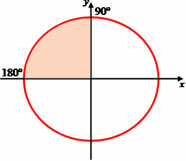
The trigonometric cycle is an oriented circle, with a unit radius, associated with a Cartesian coordinate system. The center of the circle coincides with the origin of the Cartesian system. In this way, the circle is divided into four quadrants, identified in a counterclockwise direction from point A.

Considering x the measure of an arc in the trigonometric cycle, then the values of x, such that 0º < x < 360º, are present in the following quadrants:
First quadrant: 0º < x < 90º

Second quadrant: 90º < x < 180º
Third quadrant: 180º < x < 270º

Fourth quadrant: 270º < x < 360º

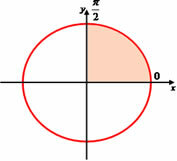
Arc values can also appear in radians, 0 < x < 2π
First quadrant: 0 < x < π/2
Second quadrant: π/2 < x < π

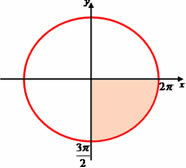
Third quadrant: π < x < 3π/2

Fourth quadrant: 3π/2 < x < 2π
It is important to know the location of the angles in the quadrants, this will facilitate the construction of trigonometric arcs, as each point in the cycle is associated with an arc. For example:
The π/6 rad or 30° measuring arc is located in the 1st quadrant.
The 3π/4 rad or 135° measuring arc is located in the 2nd quadrant.
The 7π/6 rad or 210° measuring arc is located in the 3rd quadrant.
The 5π/3 rad or 300° measuring arc is located in the 4th quadrant.
The π/3rad or 60° measuring arc is located in the 1st quadrant.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/identificando-os-quadrantes-ciclo-trigonometrico.htm