THE dimensional analysis is a tool that enables the prediction, inspection and adaptation of the physical units that are used to solve equations. In dimensional analysis, we apply the fundamentals of algebra in order to determine in which unityinmeasure some quantity must be expressed, in order to guarantee the homogeneity between the quantities.
Step-by-step dimensional analysis
Using dimensional analysis, it is possible to predict what will be the unit of measure of some physical quantity that is related to resolution of some problem. Therefore, it is necessary that we know at least the unitsfundamentals of Physics, listed in the International System of Units (SI).
From the fundamental quantities, such as the meter, the kilogram, the second and others, we can write all the other derived quantities. The table below shows some of the most important SI units – it is important to know them, check them out:
Greatness |
Unit (symbol - name) |
Length |
m - meter |
Time |
s - second |
Pasta |
kg - kilogram |
Temperature |
K - Kelvin |
Electric current |
A - Ampere |
Dimensional analysis of formulas
Let's learn how to do the dimensional analysis of a simple formula, like the average speed. Average speed is calculated as the ratio of displacement (ΔS) to time interval (Δt).
Knowing the fundamental units of the SI, it is possible to identify that the displacement must be measured in meters (m), while the time interval must be measured in seconds (s). Thus, the speed measurement unit must be given in meters per second (m/s), see the figure below:
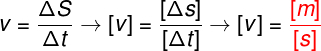
See too: Check out solved exercises on uniform movement
In the dimensional analysis, performed previously, realize that it was necessary to know the distance and time units, so that we could predict what the unit of velocity should be. Furthermore, since the formula indicated that the distance and time quantities were divided by each other, their units were also divided.
Some formulas or quantities may be a little more laborious to determine their units, check out an example in which it is necessary that we know, in addition to the units, the formulas that allow us to calculate the quantities that are related to them. Below is an example of the pressure formula, in which we want to determine what the unit of P is:
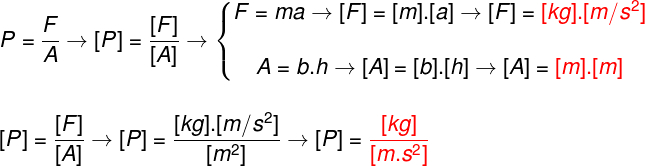
To find the unit in which the pressure must be written, according to the SI, first it was necessary for us to know your formula. After that, we would need to know in which unit the magnitude strength is expressed and if we didn't know, it would be necessary to know its formula (F=ma), to find its unit.
After that, it was necessary to remember that areas are measured in m². With these units in hand, we went back to the formula and we replace every magnitude with their respective units and we apply the rules of algebra: we do divisions and multiplications between the units to simplify them as much as possible.
An important notion in dimensional analysis is that some units can be written in line and this is common in certain exercises as the notation becomes more compact. Note the following example, in which we show the dimensional analysis of the acceleration quantity:
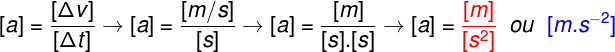
Performing the dimensional analysis of the acceleration, we find that its unit is the meter per second squared (m/s²), however, this unit can be compactly written as simply ms-2.
See too:all about acceleration
There is also the possibility that it will be necessary to determine some more physical quantity. complex, as in the example that we will show below. In it, we will make the determination of the unit of measure of the quantity called specific heat, widely used in calorimetry calculations, check out:

In the dimensional analysis presented, it was necessary to rearrange the equation in order to find what would be the expression for the specific heat ([c]). Once that's done, we keep changing the units of each physical quantity until we find two different answers: in blue, the unit of specific heat for the SI, and in red, the usual unit of specific heat.
It is possible that there is also a need to determine the unit of measure of some greatnessfictitious. In this case, we elaborate an example of a quantity Y, which is given by the product of a length ([L]), an area ([A]) and a time interval ([t]), divided by a mass ([ m]).
To determine the unit of measure of this quantity, according to the SI, it is necessary to remember that the unit of length is the meter (m), that the unit of area is the square meter (m²), that the unit of time is the second (s) and that the unit of mass is the kilogram (kg). The method used to discover the unit of Y is called the homogeneity principle, that is, the left side of the equation must have the same unit as the right side.
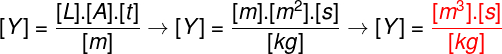
Converting Units Using Dimensional Analysis
Using dimensional analysis and correspondence between different measurement systems, it is possible to transform derived quantities such as velocity, acceleration, force, etc. Derived quantities are composed of two or more fundamental physical quantities, and sometimes it is necessary to transform them into other units. The most common example of this application of dimensional analysis is the transformation of measured velocity in meters per second to kilometers per hour and vice versa.
The key to doing this unit conversion correctly is always to multiply the unit by 1 in a convenient way: changing its unit of measure without changing its “value”. Thus, despite finding a different measure for the quantity to be converted, its scale will have been maintained. Check out an example:

In the presented conversion, we need to identify that 1 km is equal to 1000 m and that 1 h is equal to 3600 s. After that, we multiply the speed value that was measured in kilometers per hour, by 1, that is, 1000 m divided by 1 km and 1 h divided by 3600 s. In this way, it was possible to change the unit and find out what the module of this speed would be in the unit of meters per second.
See too: All about Newton's Laws
Dimensional analysis in Enem
There are several Enem issues in which it is necessary to make use of dimensional analysis for the conversioninunits correctly. However, Enem's questions will not make this explicit most of the time. It will be necessary to realize that the units are inconsistent, that is, non-homogeneous.
Check out some examples of Enem exercises that involve dimensional analysis:
Question 1) The map on the side represents a neighborhood in a certain city, in which the arrows indicate the direction of the traffic's hands. It is known that this neighborhood was planned and that each block represented in the figure is a square plot, with a side equal to 200 meters. Disregarding the width of the streets, what would be the time, in minutes, that a bus, at constant speed and equal to 40 km/h, departing from point X, would take to reach point Y?
a) 25 min
b) 15 min
c) 2.5 min
d) 1.5 min
e) 0.15 min
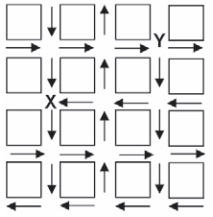
To solve this exercise, we will use the average speed formula. According to the statement, the speed of the bus is 40 km/h and we want to discover the time necessary, in minutes, so that it leaves point X and arrives at point Y, respecting the directions of each way. To do so, it will be necessary to determine the distance covered by the bus.
Analyzing the direction of the arrows, we find that the bus needs to move south, moving one block, then it needs to move west, walking one block, then move two more blocks north and then one block to the West. As each block is 200 m long, at the end of the route, the bus will have walked a total of 1000 m. Let's do the calculation:

To solve the exercise, we first transform the bus speed into kilometers per minute. We then found its displacement in kilometers, using dimensional analysis and comparing the quantities. Finally, we apply the values found in the average speed formula.
See too:All about the mechanics that fall in Enem
Question 2) Although the Body Mass Index (BMI) is widely used, there are still numerous theoretical restrictions on its use and on the recommended normal ranges. The Reciprocal Weight Index (RIP), according to the allometric model, has a better foundation mathematics, since mass is a variable of cubic dimensions and height is a variable of dimensions linear. The formulas that determine these indexes are:

If a girl, with 64 kg of mass, has a BMI equal to 25 kg/m2, so it has a RIP equal to:
a) 0.4 cm/kg1/3
b) 2.5 cm/kg1/3
c) 8 cm/kg1/3
d) 20 cm/kg1/3
e) 40 cm/kg1/3
To start solving this exercise, we must perform the dimensional analysis of the two quantities, the BMI and the RIP:

As we know the girl's BMI and mass, it's easy to find her height. After that, we just apply these values in the RIP formula, transforming the girl's height into centimeters, in order to calculate it.

See too: Check out how to study Physics for the Enem test
solved exercises
Question 1) Determine the dimension of the physical quantity X, defined by the dimensions shown below, according to the International System of Units:
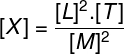
a) m-²s¹kg-²
b) m²s¹kg-²
c) m²s¹kg-3
d) m²s-¹kg-²
e) m²s¹kg-1
Template: Letter B
Resolution:
To solve the exercise, we must remember that L designates the quantity length, defined in meters, T is used to designate the time quantity, measured in seconds, and M is used to designate the mass quantity, measured in kilograms. In this way, it is enough to replace these quantities in their respective dimensions:
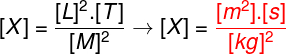
By writing this unit in line, we will have the following result: m².s¹.kg-2.
Question 2) Determine what the unit of the electrostatic constant should be k0, according to Coulomb's Law:
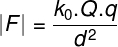
Where Q and q are measured in C – Coulomb, d is the distance measured in m – meters and F is the electric force, measured in N – Newton. So, to find the unit of k0, we must do the following dimensional analysis:
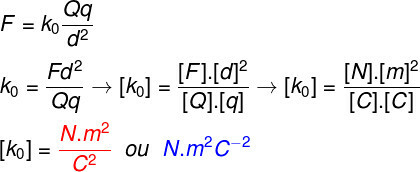
Therefore, according to the dimensional analysis carried out, the unit of measure of the constant k0 is the Nm2.Ç-2.
By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/analise-dimensional.htm

