Operations with fractions, that is, with the set of rational numbers, they are part of a set closed to operations in addition, subtraction, multiplication and division.
In math, when we say that a set is closed for some operation, we mean that when we operate two any elements of this set, the result still remains in it, that is, when we perform any operation between fractions, O result is still a fraction.
Read too: Mixed numbers: learn how to solve problems with them!
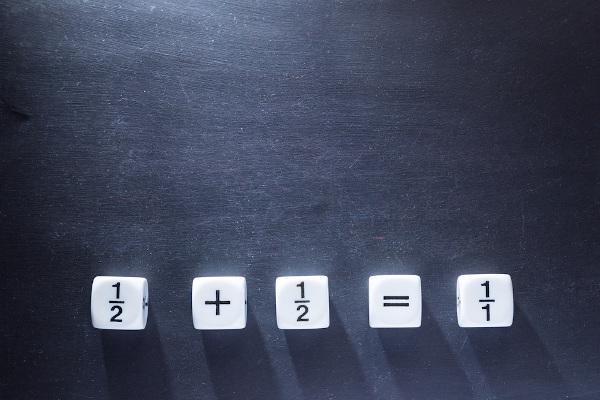
adding fractions
The idea of adding fractions is identical to adding whole numbers. To better understand the first type, let's compare the following images.

realize two 1/4 partsequate The 1/2. I.e:

The use of graphic elements aids in understanding how to add fractions, however, it is not convenient to draw drawings every time we want to add two or more of these.
Do not stop now... There's more after the advertising ;)
From the last example, see that if we calculate the
least common multiple of the denominators, we divide that number then by the denominators and then multiply what is left by the numerators, we get 1/2. Check out:
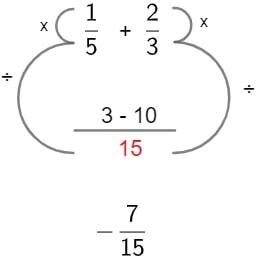
Fraction subtraction
The idea of subtraction is practically identical to the addition operation.. We will use the same algebraic process, however, instead of adding the denominators, we will subtract them. Look:
Read too: Fraction reduction to the same denominator
Fraction multiplication
THE multiplication between fractions consists of multiplying numerator with numerator and then, denominator with denominator from them. Generally speaking, the multiplication looks like this:

Don't forget that, at the end of all fractions, we must simplify them if possible. See the example:

division of fractions
At fraction division, we must conserve (keep) the first fraction and multiply it by the inverse of the second. Its general form is as follows:

The division of fractions presents two notations, that is, two different ways of representing the same idea, they are:
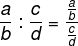
Example:
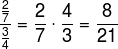
solved exercises
question 1 - Add 3/5 to 3/6, and divide the result obtained by the inverse of the number 30.
Solution:
Initially we must add the fractions of the statement, like this:
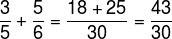
Now, according to the statement, we should divide this result by the inverse of 30, that is, 1/30. Thus:
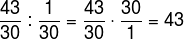
Result = 43
question 2 - What happens when multiplying any fraction by its inverse?
Solution
Note that we have two ways to think about this exercise. The first one: multiplying a fraction by the inverse is the same as dividing it. So, by dividing two equal numbers, the result can only be equal to 1. The second: multiply a fraction by its inverse, see:
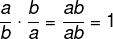
by Robson Luiz
Maths teacher
Would you like to reference this text in a school or academic work? Look:
LUIZ, Robson. "Operations with fractions"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/fracao-as-operacoes-matematicas.htm. Accessed on June 28, 2021.
1st degree equation, Equation, Equivalent equation, Equality, Mathematical equality, Principles of equality, Additive principle of equality, Multiplication principle of equality.