THE modular equation is a equation that, in the first or second member, has terms in module. The modulus, also known as the absolute value, is linked to the distance a number has to zero. Since we are talking about distance, the modulus of a number is always positive. Solving modular equation problems requires applying the modulus definition, we usually divide the equation into two possible cases:
when what is inside the module is positive and
when what is inside the module is negative.
Read too: What is the difference between a function and an equation?
one real number module

In order to be able to solve modular equation problems, it is necessary to remember the modulo definition. The module is always the same as distance a number has to zero, and to represent the modulus of a number no, we use the straight bar as follows: |no|. To calculate the |no|, we divided into two cases:
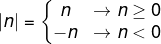
Therefore, we can say that |no| it's the same no when it is a positive number or equal to zero, and, in the second case, |
no| is equal to the opposite of no if it is negative. Remember that the opposite of a negative number is always positive, so the |no| always has a result equal to a positive number.Do not stop now... There's more after the advertising ;)
Examples:
a) |2| = 2
b) |-1| = -(-1) = 1

See too: How to solve logarithmic equation?
How to solve a modular equation?
To find the solution of a modular equation, it is necessary to analyze each one of the possibilities, that is, to divide, always in two cases, each one of the modules. In addition to knowing the modulus definition, to solve modular equations, it is essential to know how to solve polynomial equations.
Example 1:
|x – 3| = 5
To find the solution to this equation, it is important to remember that there are two possible outcomes that make |no| = 5, that's them, no = -5, since |-5| = 5, and also no = 5, because |5| = 5. So, using this same idea, we have to:
I → x – 3 = 5 or
II → x – 3 = -5
Solving one of the equations separately:
Resolution I:
x – 3 = 5
x = 5 + 3
x = 8
Resolution II:
x – 3 = -5
x = -5 + 3
x = -2
So there are two solutions: S = {-2, 8}.
Note that if x = 8, the equation is true because:
|x – 3| = 5
|8 – 3| = 5
|5| = 5
Also note that if x = -2, the equation is also true:
|-2 – 3| = 5
|-5| = 5
Example 2:
|2x + 3| = 5
As in example 1, to find the solution, it is necessary to divide it into two cases, according to the module definition.
I → 2x + 3 = 5
II → 2x + 3 = -5
Resolution I:
2x + 3 = 5
2x = 5 - 3
2x = 2
x = 2/2
x = 1
Resolution II:
2x + 3 = -5
2x = -5 - 3
2x = -8
x = -8/2
x = -4
Then the set of solutions is: S = {1, -4}.
Example 3:
|x + 3| = |2x – 1|
When we have the equality of two modules, we need to divide it into two cases:
1st case, first and second member of the same sign.
2nd case, first and second member of opposite signs.
Resolution I:
We will make the two sides greater than zero, that is, we will simply remove the modulus. We can also do with both negatives, but the result will be the same.
X + 3 ≥ 0 → |x + 3| = x + 3
2x – 1 ≥ 0 → |2x – 1| = 2x - 1
x + 3 = 2x - 1
x – 2x = -1 – 3
x = -4 (-1)
x = 4
Resolution II:
Sides of opposite signs. We will choose one side to be positive and the other side to be negative.
Choosing:
|x + 3| ≥ 0 → |x + 3| = x + 3
|2x – 1| < 0 → |2x –1| = – (2x – 1)
So, we have to:
x + 3 = – (2x – 1)
x + 3 = – 2x + 1
x + 2x = - 3 + 1
3x = -2
x = -2/3
So, the set of solutions is: S = {4, -2/3}.
Also access: What are irrational equations?
solved exercises
Question 1 - (UFJF) The number of negative solutions of the modular equation |5x – 6| = x² is:
A) 0
B) 1
C) 2
D) 3
E) 4
Resolution
Alternative E
We want to solve the modular equation:
|5x – 6| = x²
So, let's split it into two cases:
Resolution I:
5x – 6 > 0 → |5x – 6| = 5x - 6
So, we have to:
5x - 6 = x²
-x² + 5x – 6 = 0
Remember that the delta value tells us how many solutions the quadratic equation has:
a = -1
b = 5
c = -6
Δ = b² - 4ac
Δ = 5² – 4 · (-1) · (-6)
Δ = 25 – 24
Δ = 1
Since 1 is positive, then in this case there are two real solutions.
Resolution II:
|5x – 6| < 0 → |5x – 6| = – (5x – 6)
– (5x – 6) = x²
– 5x + 6 = x²
– x² – 5x + 6 = 0
Δ = b² - 4ac
Δ = (-5)² – 4 · (-1) · (+6)
Δ = 25 + 24
Δ = 49
Since Δ is positive in this case too, then there are two real solutions, so the total of real solutions is 4.
Question 2 - (PUC SP) The solution set S of the equation |2x – 1| = x - 1 is:
A) S = {0, 2/3}
B) S = {0, 1/3}
C) S = Ø
D) S = {0, -1}
E) S = {0, 4/3}
Resolution
Alternative A
Resolution I:
|2x – 1| = 2x - 1
So, we have to:
2x - 1 = x - 1
2x - x = - 1 + 1
x = 0
Resolution II:
|2x – 1| = – (2x – 1)
– (2x – 1) = x – 1
-2x + 1 = x - 1
-2x - x = -1 - 1
-3x = -2 (-1)
3x = 2
x = 2/3

