We usually associate work with some physical effort made while performing a task, such as when we move an object, drag a wardrobe, wash dishes, etc. It is for this reason that we say that the measure of work performed is very subjective, but physics defines very precisely what work is.
Work performed by a constant force is nothing more than the product of force and displacement. As force and displacement are vector quantities, in which both have modulus, direction and direction, work is defined as the dot product of force. F by displacement d. Mathematically we have:
T =  .
. 
As we know, work is a scalar quantity obtained by the scalar product between two vectors. Its SI unit is the joule (1J = 1 N.m).
The work to raise an object to a certain height is independent of the path. In many cases, we choose a path where the force will be less (the Egyptians, for example, used the inclined plane, among other techniques, in the construction of the pyramids).
Work performed by various forces

As seen before, in order to determine the work of a force, it is enough to make the product of the force by the displacement. When there are several forces being applied to an object, in order to determine the total work done on it, it is necessary to add up all the work carried out by each of the forces. See the figure above.
You can determine the work of various forces in two ways:
- the first one is finding the net force and calculating its work;
- the second is adding the work of each of the forces independently of the others.
The first way can be written as a function of net force and displacement. So we have:
T =  R.
R. 
In the equation above, 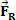 is the resulting force.
is the resulting force.
 R =
R =  1 +
1 +  2 +
2 +  3 +... +
3 +... +  no
no
Which is equivalent to carrying out the sum of the work carried out by each force separately:
T = 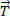 1 +
1 + 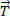 2 +
2 + 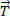 3 + ... +
3 + ... + 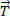 no
no
Or yet:
T =  1.
1.  +
+  2.
2.  +
+  3.
3.  + ... +
+ ... + no.
no. 
We can conclude that the two ways result in the same value for the total work.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/trabalho-realizado-por-varias-forcas.htm

