You liquids can suffer thermal expansion, as well as solids, when heated. The expansion of liquids occurs when their temperature increases, so that its molecules are more agitated. To determine the dilation of a liquid's volume, we need to know its volumetric expansion coefficient, but also the dilation suffered by the container that contains this liquid.
The dilation suffered by liquids is called volumetric dilation. In this type of dilation, all dimensions of a body or fluid, like liquids and gases, undergo significant increases in response to an increase in temperature. This phenomenon arises because of the thermal agitation of the body's molecules: the higher the temperature, the greater the amplitude of the agitation of these molecules, which start to move in a larger space.
Lookalso: Basic Concepts of Hydrostatics
Volumetric expansion formula
We can calculate the volumetric expansion suffered by a liquid using the following formula:

ΔV — volume variation (m³)
V0— initial volume (m³)
γ — volumetric expansion coefficient (°C-1)
ΔT — temperature variation (°C)
The formula shown above can be used to calculate the increase in volume (ΔV) of a liquid due to a variation in its temperature (ΔT). With some algebraic manipulations, it is possible to write the same formula as above in a format that allows us to directly calculate the final volume of a liquid after heating it, see:

V — final liquid volume
Note that, in both formulas, it is necessary to know how much the constant γ, known as volumetric expansion coefficient. This magnitude, measured in ºC-1(It reads: 1 on degrees Celsius), it gives us how great is the expansion of some substance, for every 1°C of change in its temperature.
Volumetric expansion coefficient
The volumetric expansion coefficient is a physical property which measures how large a body's volume change is for a given change in its temperature. This quantity is not constant, and its value can be considered constant for only some temperature ranges. Check out some typical values of the expansion coefficients of some substances in the liquid state, at a temperature of 20 °C:
Substance |
Volumetric expansion coefficient (°C-1) |
Water |
1,3.10-4 |
Mercury |
1,8.10-4 |
Ethyl alcohol |
11,2.10-4 |
Acetone |
14,9.10-4 |
Glycerin |
4,9.10-4 |
As stated above, the volumetric expansion coefficient has dependency with the temperature, that is, your module may fluctuate during warm-up or cool-down. Therefore, to make the calculations, we use the expansion coefficients that are within the temperature ranges, where the graph of V x T has the format linear. Watch:
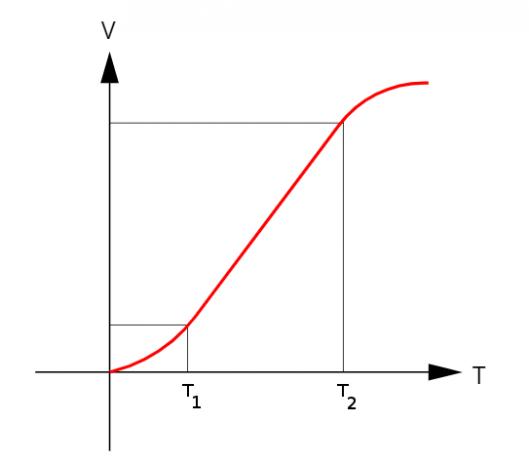
Between temperatures T1 and T2, the coefficient of expansion is constant.
Apparent dilation of liquids
The apparent expansion of liquids is determined by the volume of liquid that is overflowed if a container completely full of this liquid is heated. However, if the container experiences a volume variation equal to the volumetric variation suffered by the liquid, no liquid should overflow.

The volume of liquid overflowed in the figure corresponds to the apparent expansion.
Apparent Dilation Formulas
In order to calculate the volume of liquid that overflows from the bottle, we must use the formula of apparent dilation, note:
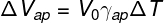
ΔVap — apparent dilation (m³)
V0 — initial liquid volume (m³)
γap — apparent volumetric expansion coefficient (°C-1)
ΔT — temperature variation (°C)
In the formula above, ΔVap corresponds to the volume of liquid overflowed, while γap is the apparent expansion coefficient. In order to know how to calculate the apparent expansion coefficient, we must take into account the expansion suffered by the flask (ΔVF) that contained the liquid. To do so, we will use the following formula:
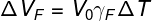
ΔVF — bottle expansion (m³)
V0— initial volume of the bottle (m³)
γF — coefficient of volumetric expansion of the flask (°C-1)
ΔT — temperature variation (°C)
In the previous expression, γF refers to the coefficient of volumetric expansion of the container containing the liquid, and ΔVF measures what was the dilation of that bottle. In this way, the actual expansion suffered by the liquid (ΔVR) can be calculated as the sum of the apparent dilation with the vial dilation, note:

ΔVR—actual liquid dilation
ΔVap — apparent liquid dilation
ΔVR — actual vial dilation
After some algebraic manipulations with the formulas presented, it is possible to reach the following result:

γ — real liquid expansion coefficient (°C-1)
γF — coefficient of volumetric expansion of the flask (°C-1)
γap — apparent volumetric expansion coefficient (°C-1)
The above relationship indicates that the actual expansion coefficient of the liquid can be found using the sum between the apparent dilation coefficients it's the flask expansion coefficient.
anomalous dilation of water
The water has a anomalous behavior regarding the thermal expansion between the temperatures of 0°C and 4°C, understand: heating the water from 0°C to 4°C, your volume decreases, instead of increasing. For this reason, in the liquid state, the density of the water has your highest value for the temperature of 4°C. The graphs below help to understand the behavior of density and volume of water as a function of its temperature, note:
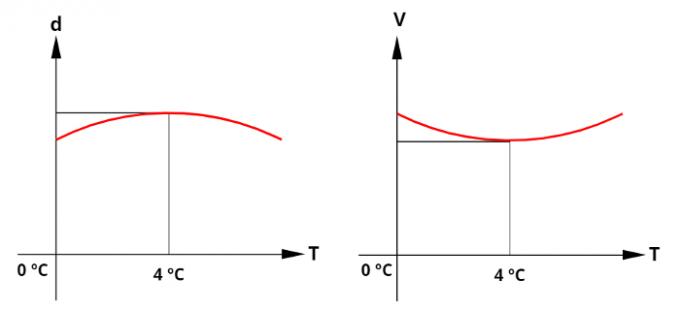
At a temperature of 4°C, the density of water is the highest.
As a result of this behavior, soft drinks or bottles of water burst when left in the freezer for too long. When the water reaches the temperature of 4°C, its volume is minimally occupied by liquid water, if cooling continues, the water volume will increase instead of decrease. when the water reaches 0°C, the volume of water will have increased greatly, while its container will have reduced its own measurements, causing its break.

Bottles filled with water that go to the freezer can burst when they reach 0°C.
Another consequence of this anomalous behavior of water is the no freezing of river bottoms in very cold regions. When the water temperature approaches 0 ºC, its density decreases, and then the cold water rises, due to the buoyancy. As it ascends, the cold water freezes, forming a layer of ice over the rivers. as ice is a good thermal insulator, the bottom of the rivers remains at approximately 4 ºC, because, at this temperature, its density is maximum and tends to remain at the bottom of the rivers.
The reason behind the anomalous behavior of water has a molecular origin: between 0 °C and 4 °C, the electrical attraction between the water molecules overcome thermal agitation, due to the existence of hydrogen bonds present between the water molecules. Water.
Lookalso: How does anomalous water expansion occur?
solved exercises
1) Determine the volumetric expansion coefficient of a 1 m³ portion of liquid that undergoes a 0.05 m³ expansion when heated from 25°C to 225°C.
Resolution:
Let's calculate the expansion coefficient of the liquid in question using the volumetric expansion formula:
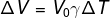
Applying the data provided by the statement to the previous formula, we will make the following calculation:
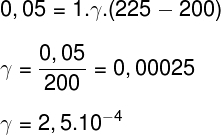
2) A glass flask, whose volumetric expansion coefficient is 27.10-6 °C-1, has a thermal capacity of 1000 ml, at a temperature of 20 ºC, and is completely filled with an unknown liquid. When we heat the set up to 120 ºC, 50 ml of liquid overflows out of the container. Determine the apparent expansion coefficients; the actual expansion coefficient of the liquid; and the dilation suffered by the glass vial.
Resolution:
Let's calculate the apparent expansion coefficient, for that, we'll use the following formula:
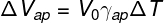
Using the exercise data, we will do the following calculation:

Next, we will calculate the liquid's actual expansion coefficient. To do so, we need to calculate what was the dilation suffered by the glass bottle:

Replacing the data provided by the exercise statement, we have to solve the following calculation:

With the calculation above, we determined what was the expansion suffered by the glass flask. Thus, to find the real expansion of the liquid, just add the volume of the apparent dilatation to the volume of the flask's expansion:

The result obtained in the answer above indicates that the liquid inside the bottle underwent an actual expansion of 52.7 ml. Finally, let's calculate the liquid's real expansion coefficient:

Using the above formula, we calculate the real water expansion coefficient equal to:

Therefore, the coefficient of thermal expansion of this liquid is 5.27.10-4 °C-1.
By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/dilatacao-liquidos.htm