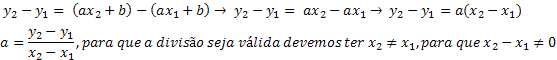The equation is characterized by the equal sign (=). The inequality is characterized by the signs of greater (>), less (• Given the function f (x) = 2x – 1 → 1st degree function.
If we say that f (x) = 3, we will write it like this:
2x - 1 = 3 → 1st degree equation, calculating the value of x, we have:
2x = 3 + 1
2x = 4
x = 4: 2
x = 2 → x must be 2 for the equality to be true.
• Given the function f (x) = 2x – 1. If we say that f (x) > 3, we write it like this:
2x - 1 > 3 → 1st degree inequality, calculating the value of x, we have:
2x > 3 + 1
2x > 4
x > 4: 2
x > 2 → this result says that for this inequality to be true, x must be greater than 2, that is, it can assume any value, as long as it is greater than 2.
Thus, the solution will be: S = {x  R | x>2}
R | x>2}
• Given the function f(x) = 2(x – 1). If we say that f (x) ≥ 4x -1 we will write it like this:
2(x - 1) ≥ 4x -1
2x - 2 ≥ 4x - 1 → joining similar terms we have:
2x - 4x ≥ - 1 + 2
- 2x ≥ 1 → multiplying the inequality by -1, we have to invert the sign, see:
2x ≤ -1
x ≤ - 1: 2
x ≤ -1→ x will assume any value as long as
2 is equal to or less than 1.
So the solution will be: S = { x
 R | x ≤ -1}
R | x ≤ -1} 2
We can solve the inequalities in another way, using graphics, see:
Let's use the same inequality of the previous example 2(x – 1) ≥ 4x -1, solving it will look like this:
2(x - 1) ≥ 4x -1
2x - 2 ≥ 4x - 1
2x - 4x ≥ - 1 + 2
-2x – 1 ≥ 0 → we call -2x – 1 of f(x).
f (x) = - 2x – 1, we find the zero of the function, just say that f (x) = 0.
-2x – 1 = 0
-2x = 0 + 1
-2x = 1 (-1)
2x = -1
x = -1
2
So, the solution of the function will be: S = { x
 R | x = -1 }
R | x = -1 } 2
To build the graph of the function f (x) = - 2x – 1 just know that in this function
a = -2 and b = -1 and x = -1, the value of b is where the line passes on the y axis and the value of x is
2
where the line cuts the x axis, so we have the following graph:
So, we look at the inequality -2x – 1 ≥ 0, when we pass it to the function we find that
x ≤ - 1, so we come to the following solution:
2
S = { x
 R | x ≤ -1 }
R | x ≤ -1 } 2
Do not stop now... There's more after the advertising ;)
by Danielle de Miranda
Brazil School Team
1st Degree Euquation - Roles
Math - Brazil School Team
Would you like to reference this text in a school or academic work? Look:
RAMOS, Danielle de Miranda. "First degree polynomial inequalities"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/inequacoes-polinomiais-1-grau.htm. Accessed on June 28, 2021.