O pyramid volume is calculated by multiplying the base area and the height, dividing by three. To calculate the volume of the pyramid, it is necessary to know which polygon forms the base of this pyramid, that's why, for each base, we use a different formula to find the your area. We can relate the volume of the prism to the volume of a pyramid of the same height and area as the base, since the volume of the pyramid is equal to one third of the volume of the prism.
Read too: What are geometric shapes?
How is the volume of the pyramid calculated?

The volume of the pyramid can be calculated by a formula that directly depends on the polygon which forms the basis. To calculate the volume of any pyramid, we use the following formula:
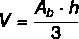
V → volume
THEB → area at the base of the pyramid
H → pyramid height
The base of a pyramid can be formed by any polygon., so we can have a triangular base pyramid, square base pyramid, hexagonal base pyramid. Anyway, any polygon can be the base of the pyramid, and as it is a polygon, to calculate the area of its base, there is a specific formula.
Read too: What are Plato's solids?
square base pyramid
In a square-based pyramid, we know that the area of the square is calculated by the length of the squared side, that is, A = there². So, to calculate the volume of a square pyramid, we calculate the product of the square of the base edge and the height of the pyramid, and divide by three. See an example below.
Example:
Calculate the volume of the pyramid below, knowing that its base is formed by a square:

In the pyramid, the height h measures 6 cm and the edge of its base measures 3 cm.
Then, we will first calculate the area of the base AB. The area of the square is equal to there², so we have to:
THEB = there²
THEB = 3²
THEB = 9 cm²
Now that we know the base area value, just replace the height measurement and the base area measurement in the pyramid volume formula:
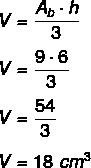
Pyramid with a triangular base
When the base of the pyramid is triangular, to calculate the area of the base, we use the formula of area of a triangle, which is equal to the product of the base and the height divided by two.
Example:
Knowing that the following pyramid is 9 cm high, calculate its volume:

As the base is a triangle, we will first calculate the area of the base, which is the length of the base times the length of the height of the triangle that forms the base, dividing by two.

Now that we know the base area value, it becomes possible to calculate the volume of this pyramid:
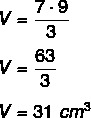
Example 2:
When the base of the pyramid is a equilateral triangle, we can use the formula for the area of the equilateral triangle to calculate the area of the base.
We will calculate the volume of a pyramid whose base is an equilateral triangle with sides measuring 8 cm, and its height measuring 15 cm.
First we calculate the area of the base, as it is an equilateral triangle, we will use the formula for the area of an equilateral triangle.

Now let's calculate the volume:
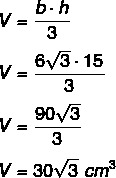
See too: Differences between flat and spatial figures
Hexagonal base pyramid
In the hexagonal base pyramid, to calculate the base area, we use the hexagon area formula.
Example:
Calculate the volume of the pyramid knowing that its base is a regular hexagon:

First we will calculate the area of the hexagon:
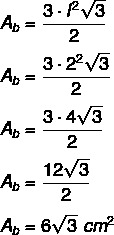
Now let's calculate the volume:

Relationship between pyramid volume and prism volume
given one prism and a pyramid of the same base, we know that the prism volume is equal to the product of the base area and the height, and the volume of the pyramid is the product of the base area and the height divided by three, so if the base area is the same, the volume of the pyramid it will be equal to 1/3 of the prism volume.

solved exercises
Question 1 - Seeking to innovate in packaging design, a cosmetic industry decided to produce packaging in the shape of a pyramid with a square base for its new moisturizer. The base of this pyramid is shaped like a square of sides measuring 6 cm. Knowing that this moisturizer must contain 200 ml, the height of the pyramid must be approximately:
A) 15.2 cm
B) 15.8 cm
C) 16.4 cm
D) 16.7 cm
E) 17.2 cm
Resolution
Alternative D
We know that 200 ml is equal to 200 cm³, so we have V = 200. So, calculating the base area, which is a square, we have to:
THEB = l²
THEB = 6²
THEB = 36 cm²
Now let's make the volume equal to 200 cm³, so we have to:

Question 2 - (Enem) A factory produces regular quadrangular pyramid-shaped paraffin candles with a height of 19 cm and a base edge of 6 cm. These candles are formed by 4 blocks of the same height — 3 pyramid trunks with parallel bases and 1 pyramid at the top — spaced 1 cm apart, being that the upper base of each block is equal to the lower base of the superimposed block, with an iron rod passing through the center of each block, joining them, as shown in the figure.

If the factory owner decides to diversify the model, removing the pyramid at the top, which is 1.5 cm edge at the base, but keeping the same mold, how much will he spend on paraffin to manufacture a candle?
A) 156 cm³
B) 189 cm³
C) 192 cm³
D) 216 cm³
E) 540 cm³
Resolution
Alternative B
Let's calculate the difference between the larger pyramid (V) and the smaller pyramid (V2).
We know that there is 1 cm of distance between the blocks, so the height of the biggest pyramid is 19 – 3 = 16 cm. The larger pyramid is 6 cm from the base, as the base is a square, so AB = l² = 6² = 36.
Thus, the volume of the larger pyramid is:
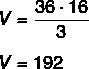
To find the height of the smallest pyramid, let's divide the total height by 4, so 16: 4 = 4 cm. Doing the same with the edge, we get 6: 4 = 1.5.
Thus, the area of the base of the smaller pyramid is 1.5² = 2.25. Calculating the volume, we have to:
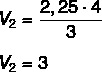
Now we find the difference between volumes:
192 - 3 = 189 cm³
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/volume-piramide.htm

