Geometry is present in situations involving measurements of length, area and volume. It is considered a specific branch of Mathematics. Let's focus our study on calculating areas of irregular figures.
Every regular figure has a mathematical expression responsible for calculating its area, but in cases in that the figure has an irregular shape, the calculation of its surface area occurs in a way Special. Look at the figure below, it represents the surface of an irregular region:

To calculate its area, we must transpose the figure onto squared paper, as follows:

1st step: count the number of whole squares that fill the inside of the figure. The area missing from the figure is 43 squares (figure A).
2nd step: count the number of whole squares that cover the entire figure. The excess area of the region is 80 squares (figure B).
To determine the approximate area of the figure, which is between 43 and 80, we used an arithmetic average of the number of grids found:
approximate area
Do not stop now... There's more after the advertising ;)

The unit of area used will be that of the figure in its original size. In this case, the area of the given figure is in m², so each grid represents 1 m². Therefore, the area of the irregular region is approximately 61.5 m².
Example 2
Determine the area of the highlighted irregular region, using the grid as the unit of area.
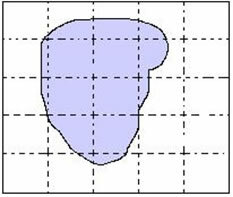
The area for lack of the given irregular region constitutes the amount of entire squares inside it, which corresponds to 4 squares.
The excess area of the region constitutes the amount of squares that cover the figure, corresponding to 15 squares.
We will determine the area of the figure through the arithmetic mean between 4 and 15.

The area of the figure is approximately 9.5 area units.
by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Calculation of Special Areas"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/calculo-de-areas-especiais.htm. Accessed on June 28, 2021.