Calculating the probability of simultaneous events determines the chance of two events occurring simultaneously or successively.
The formula for calculating this probability derives from the conditional probability formula. Thus, we will have: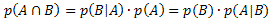
If events A and B are independent, that is, if the fact that event B occurs does not change the probability of event A occurring, the formula for calculating the conditional probability is: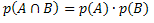
Let's do some examples to explore the use of the formula and the correct way to interpret problems related to the probability of simultaneous events.
Example 1. On two successive rolls of the same die, what is the probability of a number greater than 3 and the number 2 occurring?
Solution: realize that the occurrence of one event does not influence the probability of another one occurring, so they are two independent events. Let's distinguish the two events:
A: output a number greater than 3 → we have as possible results the numbers 4, 5 or 6.
B: exit number 2
Let's calculate the probability of occurrence of each of the events. Note that when rolling a die, we have 6 possible values. Thus:
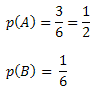
In this way, we will have:
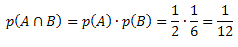
Example 2. In an urn there are 30 balls numbered from 1 to 30. Two balls will be randomly removed from this urn, one after the other, without replacement. What is the probability that a multiple of 10 will come out in the first and an odd number in the second?
Solution: the fact that the pellets are removed without replacement, implies that the occurrence of the first event interferes with the probability of the second. Therefore, these events are not independent. Let's determine each of the events.
A: output a multiple of 10 → {10, 20, 30}
B: output an odd number → {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29}
The probability of occurring the two events successively will be given by:
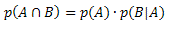
We will do the calculations separately:
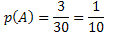
For the calculation of p (B|A) it is necessary to note that we will no longer have 30 balls in the urn, as one was removed and there was no replacement, leaving 29 balls in the urn. Thus,
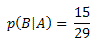
Soon,

Do not stop now... There's more after the advertising ;)
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Probability - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Probability of simultaneous events"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/probabilidade-eventos-simultaneos.htm. Accessed on June 28, 2021.