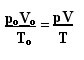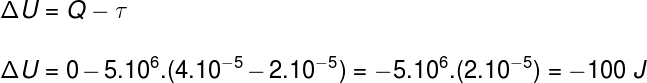In the study of Physics, to be well characterized, there are quantities whose measurements need the identification of their intensity, a number accompanied by a unit of measure, and their orientation in the space where they are. Such quantities are called vector quantities. As an example of a vector quantity there is the displacement, for, to describe it, we need the distance covered by the mobile, as well as its direction and meaning.
There are several vector quantities, here are some of them: velocity, displacement, position, momentum and acceleration.
In our studies related to varied motions, we could see the simple definition of the mean scalar acceleration. Such acceleration is defined as the quotient between the variation of the scalar velocity (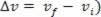
and the respective time interval (
.
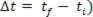In a similar way, we have the possibility to define the average vector acceleration. Let's consider that a piece of furniture currently has t1 a speed v1and in the instant t2 have a speed v2. The average vector acceleration is defined as follows:
Do not stop now... There's more after the advertising ;)
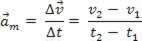
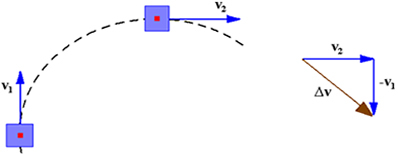
By the polygon rule, we obtain the velocity variation vector (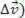
. Let's see the figure below:
So we can write:
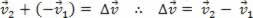
- The instantaneous vector acceleration (
) can be understood as being an average vector acceleration, when the time interval Δt is infinitely small.
- Whenever there is a variation in the vector velocity, 
, there will be vector acceleration .
By Domitiano Marques
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
SILVA, Domitiano Correa Marques da. "Average vector acceleration"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/aceleracao-vetorial-media.htm. Accessed on June 27, 2021.
