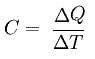Energymechanics is physical quantity climb, measured in joules, according to the SI. It is equivalent to the sum of the kinetic and potential energies of a physical system. In conservative systems, that is, without friction, the mechanical energy remains constant.
See too:Electrostatics: what is electrical charge, electrification, static and other concepts
Introduction to Mechanical Energy
When a particle with mass movesfreely through space, for sure velocity and without suffering the action of strength some, we say that it carries with it a quantity of pure energykinetics. However, if this particle starts to undergo some kind of interaction (gravitational, electric, magnetic or elastic, for example), we say that it also has a energypotential.
Potential energy is therefore a form of energy that can be stored or stored; while kinetic energy is that relative to the particle's velocity.
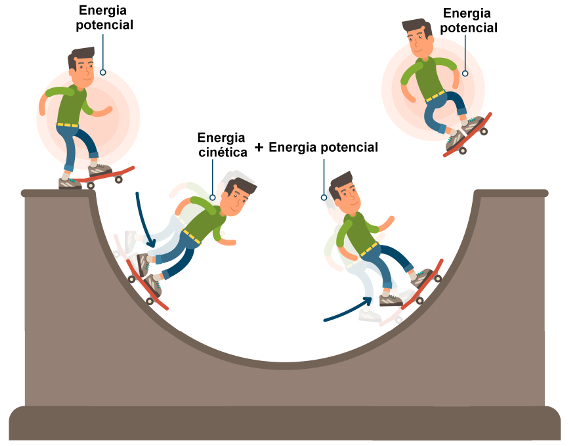
Now that we have defined the concepts of kinetic energy and potential energy, we can understand more clearly what mechanical energy is all about: it is the totality of energy related to the state of movement of a body.
See too: Elements, formulas and main concepts related to electrical circuits
Mechanical energy formulas
The formula of energykinetics, which relates to pasta (m) and the velocity (v) of the body, this is it, check:

ANDÇ - kinetic energy
m - pasta
v - velocity
P – amount of movement
THE energypotential, in turn, it exists in different forms. The most common, however, are gravitational and elastic potential energies, whose formulas are shown below:

k – elastic constant (N/m)
x – deformation
While the gravitational potential energy, as its name suggests, is related to the local gravity and the height at which a body is in relation to the ground, the energypotentialelastic it arises when some elastic body is deformed, as when we stretch a rubber band.
In this example, all the potential energy is “stored” in the rubber band and can be accessed later. To do so, just release the strip so that all the elastic potential energy is transformed into kinetic energy.
The sum of these two forms of energy — kinetic and potential — is called mechanical energy:

ANDM – mechanical energy
ANDÇ - kinetic energy
ANDP - potential energy
Do not stop now... There's more after the advertising ;)
Conservation of mechanical energy
THE energy conservation is one of the principles of physics. According to him, the total amount of energy in a system must be conserved. In other words, the energy is never lostorcreated, but rather converted into different forms.
Of course, the principle of conservation of mechanical energy derives from the principle of energy conservation. We say that mechanical energy is conserved when there aren't anydissipative forces, such as friction or drag of the air, capable of transforming it into other forms of energy, such as thermal.

check out examples:
When a heavy box slides over a friction ramp, part of the kinetic energy of the box is dissipated, and then the interface between the box and the ramp suffers a little increase of temperature: It's as if the kinetic energy of the box is being transferred to the atoms at the interface, causing them to oscillate more and more. The same happens when we step on the brake of a car: the brake disc gets hotter and hotter, until the car comes to a complete stop.
See too:What is friction force? Check out our mind map
In a ideal situation, wherein movement occurs without the action of any dissipative forces, mechanical energy will be conserved. Imagine a situation where a body swings freely without any friction with the air. In this situation, two points A and B, relative to the position of the pendulum, follow this relationship:

ANDBAD – Mechanical energy at point A
ANDMB – Mechanical energy at point B
ANDHERE – Kinetic energy at point A
ANDCB – Kinetic energy at point B
ANDPAN – Potential energy at point A
ANDPB – Potential energy at point B
Given two positions of an ideal, frictionless physical system, the mechanical energy at point A and the mechanical energy at point B will be equal in magnitude. However, it is possible that, in different parts of this system, the kinetic and potential energies change measurement so that their sum remains the same.
See too: Newton's 1st, 2nd and 3rd Laws – Introduction, Mind Map and Exercises
Exercises on mechanical energy
Question 1) A 1500 kg truck travels at 10 m/s over a 10 m viaduct, built above a busy avenue. Determine the modulus of the truck's mechanical energy in relation to the avenue.
Data: g = 10 m/s²
a) 1.25.104 J
b) 7,25.105 J
c) 1,5105 J
d) 2.25.105 J
e) 9.3.103 J
Template: Letter D
Resolution:
To calculate the mechanical energy of the truck, we will add the kinetic energy with the gravitational potential energy, observe:

Based on the above calculation, we found that the mechanical energy of this truck in relation to the floor of the avenue is equal to 2.25.105 J, therefore, the correct answer is the letter d.
Question 2) A 10,000 l cubic water tank is filled to half its total volume and positioned 15 m above the ground. Determine the mechanical energy of this water tank.
a) 7.5.105 J
b) 1.5.105 J
c) 1.5.106 J
d) 7.5.103 J
e) 5.0.102 J
Template: Letter a
Resolution:
Once the water tank is filled to half its volume and knowing that 1 l of water corresponds to a mass of 1 kg, we will calculate the mechanical energy of the water tank. Thus, it is important to realize that, when at rest, the kinetic energy of the body is equal to 0, and therefore its mechanical energy will be equal to its potential energy.

According to the result obtained, the correct alternative is the letter a.
Question 3) Regarding the mechanical energy of a conservative system, free from dissipative forces, check the alternative correct:
a) In the presence of friction, or other dissipative forces, the mechanical energy of a moving body increases.
b) The mechanical energy of a body that moves free from the action of any dissipative forces remains constant.
c) For the mechanical energy of a body to remain constant, it is necessary that, when there is an increase in kinetic energy, there is also an increase in potential energy.
d) Potential energy is the part of mechanical energy related to the speed at which the body moves.
e) The kinetic energy of a body that moves free from the action of any dissipative forces remains constant.
Template: Letter B
Resolution:
Let's look at the alternatives:
The) FALSE - in the presence of dissipative forces, the mechanical energy decreases.
B) REAL
ç) FALSE - if there is an increase in kinetic energy, the potential energy must decrease, so that the mechanical energy remains constant.
d) FALSE - kinetic energy is the part of mechanical energy related to motion.
and) FALSE - in this case, the kinetic energy will decrease due to dissipative forces.
By Rafael Hellerbrock
Physics teacher