For solve exercises on the applications of Newton's Laws, as in block systems, it is interesting to follow a few steps:
1. Write down all relevant data from the statement;
2. Check if the units are in the International System of Units (meter, kilogram and second);
3. Carefully draw all the forces acting on bodies;
4. Try to sense in which direction the body system is moving and adopt your direction for the positive sign of the forces. All forces that are in this direction will also be positive. Counter forces will be negative;
5. Equalize the resultant of the forces of each body for each direction of space to the product bad or to 0, in the case where the body is moving with constant velocity or is at rest;
6. Remember that bodies that move together, connected by cables, one on top of the other, or even leaning against each other are mutually supportive and therefore have the same acceleration;
7. To solve the system of equations, we must subtract one from the other, as the action and reaction pairs have the same value and cancel each other out.
If you carefully follow all the steps above, you will hardly make any mistakes when solving exercises on Newton's Laws.
See too: Five Things You Need to Know About Newton's Laws
Newton's Laws Solved Exercises
NOTE: For all the examples below we will adopt gravity as 10 m/s².
question 1
Two blocks, THE and B, of masses equal to 8 kg and 2 kg, respectively, are represented in the figure below. The blocks are joined by an inextensible string and pulled by a force F of a modulus equal to 20 N. Determine:

a) System acceleration
b) Wire pull
Resolution:
1- Annotating the data
The most relevant data for the exercise are:
mThe = 2 kg;
mB = 8 kg;
|F| = 20 N.
2 - Checking the units
All units are compatible with each other and are in the International System of Units;
3-making the force diagram
Deheatingly all forces acting on each block. We must remember the force weight, normal force, tension on the wire that block A exerts on block B and the force F that is applied on block B. We are left with the following scheme:

Subtitle:
PThe = Weight of block A
PB = Weight of block B
NThe = Normal of block A
NB = Block B Normal
F = Force on the system
Tb, the = Traction that block B does on block A
T a, b = Traction that block A does on block B
4 -Orienting the coordinate system
The block system moves to the right and therefore all forces pointing in that direction will have a positive sign. Forces pointing to the left will have a negative sign.
5 -Finding the resulting forces
According to the sign adopted in step 4, the resulting forces, in the x and y directions (horizontal and vertical), for each block will be determined by:

6 -bodies move together
Note that the normal force and weight of each block cancel each other out, as the blocks do not move in the y (vertical) direction, so, N = P. Also, as the blocks move together, they have the same acceleration value.
7 – Solving the system of equations
To solve the system of equations, let's assign to the system of equations found in step 5 the values we wrote down in step 1. Remember that the weight of bodies is given by m.g (mass times gravity):

The traction that body B does on body A and the traction that body A does on body B are a pair of action and reaction, therefore, if we add the equations, these terms (Ta, b and Tb, the) must be cancelled. By doing this, we are left with:

To determine the tension in the yarn, it does not matter if we calculate the modulus of Ta, b or from Tb, the, since the two forces are a pair of action and reaction, therefore, they have the same module:
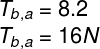
The traction exerted by the wire is 16 N.
See too: Seven Most Common Mistakes Made in the Study of Physics
Do not stop now... There's more after the advertising ;)
question 2
Two blocks, THE and B, of masses equal to 7 kg and 3 kg are connected by an inextensible wire as shown in the figure below. Calculate system acceleration and tension on both wires.

Resolution:
1 – Annotating the data
The relevant data for the exercise are:
mThe = 7 kg
mB = 3 kg
g = 10 m/s²
2 – Checking the units
All units are compatible with each other and are in the International System of Units.
3 – Making the force diagram
Let's draw all the forces present in the blocks. Look at the figure below:

Note that since body B is not supported on the table, there is no normal force on it.
4 – Orienting the coordinate system
Blocks move in directions perpendicular. Block A moves in the x direction to the right, so all forces on that block that point to the right will be positive. Block B moves in the vertical direction downwards, so all forces on this block that point downwards will be positive.
5 – Finding the resulting forces
The system of equations provided by the forces resulting from the blocks is presented below:
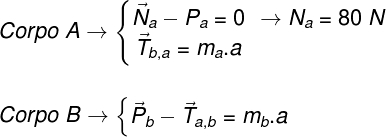
6 –bodies move together
As the bodies are connected by a wire, the acceleration is the same for both, so we only use The for the two bodies.
7 –Solving the system of equations
Remember the action and reaction pairs: Ta, b and Tb, the are canceled when we add the equations, so we are left with:

Finally, to find the tension in the wire, we can use any of the equations that involve the tensions:

With that, we find the tension in the wire, which is equivalent to 21 N.
See more at: Traction strength exercises
question 3
3. Two blocks, A and B, shown in the figure below and with masses equal to 2 kg and 3 kg, respectively, touching each other, are moved by the action of a force of 15 N on block A. Determine the acceleration of the blocks and the strength of the force that body A puts on body B.

Resolution:
1 -annotating the data
The relevant data for the exercise are:
mThe = 2 kg
mB = 3 kg
|F| = 15 N
2 - Checking the units
All units shown are in the International System of Units and are compatible with each other.
3 – Making the force diagram
Let's represent all the forces acting on the block system:

Subtitle:
PThe = Weight of block A
PB = Weight of block B
NThe = Normal of block A
NB = Block B Normal
F = Force on the block system
Fb, the = Force that block B does in block A
F a, b = Force that block A does in block B
4 -Orienting the coordinate system
The two blocks move only in the horizontal direction, and the direction of movement is to the right. Therefore, all the forces that point in this direction will be taken as positive.
5 –Finding the resulting forces
The resulting forces on blocks A and B can be written according to the orientation of item 5:

6 – bodies move together
Bodies move together because they are pressed against each other. Thus, the acceleration The it is the same for the two blocks.
7 – Solving the system of equations
To solve the system of equations, we must remember that Fa, b and Fb, the they are an action and reaction pair and cancel each other out when we add the resulting forces of A and B, so:
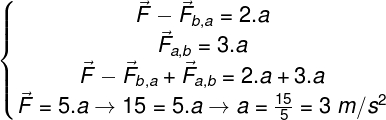
With the above system resolution, we find that the acceleration should be 3 m/s². Using any of the resulting forces found in step 5, we can determine the force that A does on B or that B does on A. These forces must have a value equal to 9 N.
By Rafael Hellerbrock
Graduated in Physics