At functionstimesofMUV are equations used to describe the trajectory of bodies that move with constant acceleration. They enable parameters to determine position, velocity or acceleration in a given instant of time, being, therefore, equations of fundamental importance for the study of the movement in the scope of çinematic.
See too:10 Essential Physics Equations for Enem
What are the MUV's time functions?
O movementevenlymiscellaneous is the one in which a body undergoes a accelerationconstant, so that its speed varies equally every second. Studying the MUV requires that we know how to use the functionstimesthe speed and theposition, which are, respectively, 1st degree functions It's from 2nd degree.

The MUV time functions are equations that depend on time as a variable.
When a piece of furniture that describes a MUV undergoes a positive variation of speed, we say that its movement is accelerated. On the other hand, if this variation is negative, we say that the movement is slowed down or retarded.
THE acceleration is one of the central concepts of MUV. This quantity can be calculated by varying the speed divided by a time interval. In the International System of Units, the unit of measurement for acceleration is the m/s², which means the change in speed, in m/s, every second.
→ Hourly function of speed in MUV
THE occupationhourlygivesvelocity of the MUV is an equation in which the mobile speed is written as a function of the instant of time. This function is a 1st degree equation, that is, it is the equation of a straight line.

v(t) – speed at time t (m/s)
v0– initial speed (m/s)
The – acceleration (m/s²)
t – instant of time(s)
Do not stop now... There's more after the advertising ;)
The figure below shows the graph of the position's hourly function, which relates velocity to time.

In the figure above, the red and blue lines represent, respectively, an accelerated movement and a delayed movement. The point at which these lines touch the vertical axis is the initial velocity of movement. Furthermore, the greater the inclination of these lines in relation to the horizontal axis, the greater the velocity module.
→ Time function of the position in the MUV
The hourly position function is the equation used to determine the position of a rover that describes a uniformly varying motion. It is a 2nd degree equation which depends on variables such as initial velocity, initial position and acceleration.
The position's hourly function is as follows:

S(t) – position at time t (m)
s0 – starting position (m)
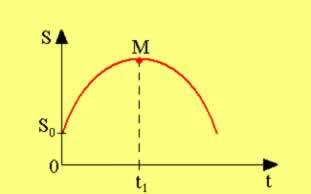
In the following figure, we show a graphic qualitative that relates the position of a body that describes a MUV in relation to time.

The graph above shows two curves, one red and one blue, which represent accelerated and delayed movements respectively. Realize that the concavity of the parable it is what defines whether the movement is accelerated or not: when the concavity is facing upwards, the acceleration is positive. On the graph, the starting position of both movements is at the point where the curves cross the vertical axis.
See too: Main concepts and formulas of uniform rectilinear movement
Solved exercises on MUV time functions
Question 1 — (UTF-PR) A cyclist moves on his bicycle, starting from rest and maintaining an approximately constant acceleration with an average value equal to 2.0 m/s². After 7.0 s of movement, it reaches a speed, in m/s, equal to:
a) 49
b) 14
c) 98
d) 35
e) 10
Resolution:
Let's solve the question and, for that, we'll use the data informed by the exercise, as well as the position's hourly function.

Based on the calculation, we find that the rover's final velocity is 14 m/s, so the correct alternative is the letter B.
Question 2 — (UFPR) A driver drives his car along the BR-277 at a speed of 108 km/h when he sees a barrier on the road, being forced to brake (deceleration of 5 m/s²) and stop the vehicle after time. It can be said that the braking time and distance will be, respectively:
a) 6 s and 90 m.
b) 10 s and 120 m.
c) 6 s and 80 m.
d) 10 s and 200 m.
e) 6 s and 120 m.
Resolution:
First let's determine what the braking time is. Note the calculation below, as we make use of the hourly velocity function:
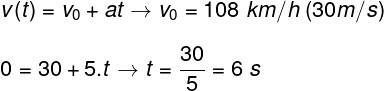
To make the above calculation, it was necessary to transform the unit of speed, which was in km/h, into m/s, dividing it by the factor 3.6. The next calculation concerns the displacement of the car to a complete stop. To do this, let's use the position's hour function:
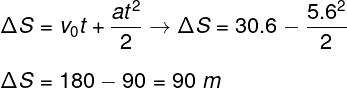
Based on the calculation, we found that the vehicle's displacement, from the start of braking to the complete stop, is 90 m. Based on this and the calculation above, the correct alternative is the letter A.
By Rafael Hellerbrock
Physics teacher