O launchvertical it is a one-dimensional movement in which the friction with the air. This type of movement occurs when a body is launched in a vertical and upward direction. The movement described by the projectile is slowed down by the acceleration of gravity until it reaches its heightmaximum. After that time, the movement is described as a fall free.
Lookalso: What is gravity?
Vertical Launch Formulas
The laws that explain the movement of bodies that do not move in the vertical direction were discovered and enunciated by the Italian physicist Galileo Galileo. In this ocasion, Galileo he realized that bodies of pastasmany different must fall with the sametime and with constant acceleration towards the ground. This situation will only be possible if the resistance force of the air acts on these bodies, dissipating their speed.
Vertical launch is a particular case of uniformly varied movement (MUV), since it occurs under the action of a constant acceleration. In this case, the acceleration of gravity opposes the projectile's launch velocity, which has sensepositive.
The equations that govern this type of movement are the same ones used for the general cases of the MUV, subject to minor changes in notation. Check out:
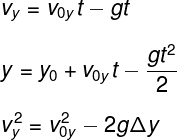
These are the three most useful equations for describing vertical throw: hourly functions of velocity and position and Torricelli's equation.
In the equations above, vy is the final height reached by the projectile for a given instant of time t. The initial speed v0y is the speed at which the projectile is launched, which can be positive, if the release is forup, or negative, if the release is forlow, i.e, in favor ofgravity. the heights Final and initial of the release are called, respectively, of y and y0. Lastly, g is the acceleration of gravity at the launch site.
It is important to remember that the equations above are defined according to the International Measurement System (SI), therefore, the speeds are given in m/s; The gravity, in m/s²; it's the time, in seconds.
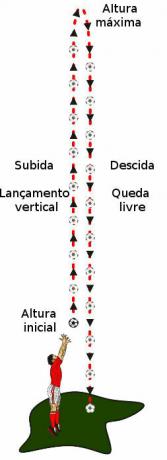
Steps in the vertical throwing movement and free fall of a ball
The equations above can be used to solve problems involving the vertical launching of projectiles. The reference chosen for these equations adopts as positive the sense forup It is like negative the sense forlow.
Do not stop now... There's more after the advertising ;)
→ Hourly function of speed
The first of the equations shown is the hourly velocity function for the vertical throw. In it, we have the final speed (vy), the projectile launch speed (v0y), the acceleration of gravity (g) and time (t):

Using the equation above, we can determine the projectile's rise time. Therefore, we must remember that, when reaching its maximum height, the vertical velocity (vy) is null. In addition, the movement changes direction, describing a free fall. Assuming the vertical velocity (vy) is null at the highest point of the vertical throw, we will have the following equality:
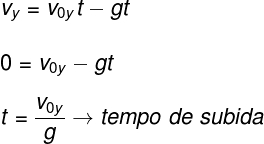
→ Position time function
The second equation shown in the image is called the hourly position function. This equation allows finding at what height (y) a projectile will be at a given instant of time (t). For this, we must know from what height the projectile was launched (H) and at what speed the launch occurred (v0y). If we replace the rise time in the variables t in this equation, it is possible to establish a relationship between the maximum height reached and the projectile's launch velocity (v0y). Look:
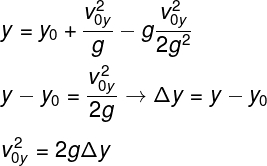
The same result shown above can be obtained if we use the Torricelli equation. To do this, just replace the final velocity term by 0, since, as stated earlier, at the highest point of the vertical throw, this velocity is null.
Free fall
When a vertically launched projectile hits its heightmaximum, starts the movement of fallfree. In this movement, the projectile falls down to the ground with accelerationconstant. In order to define the equations for this type of motion, it is interesting to define a favorable reference for the acceleration of gravity. For this, we adopted the senseforlowlikepositive and we assume that the starting position of the free fall movement is 0. In this way, the equations for free fall become simpler. Watch:
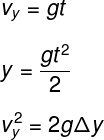
Horizontal and oblique launch
Horizontal and oblique launch are other types of projectile launch. In these cases, the difference is due to the angle of the launch in relation to the ground. Check out our articles that deal specifically with horizontal launching and oblique launching:
Horizontal release in vacuum
Oblique throw
Vertical Throw and Free Fall Exercises
1) A 2 kg projectile is launched vertically upwards from the ground at a speed of 20 m/s. Determine:
Data: g = 10 m/s²
a) the total rise time of the projectile.
b) the maximum height reached by the projectile.
c) the projectile velocity at t = 1.0 s and t = 3.0 s. Explain the result obtained.
Resolution
a) We can calculate the projectile's rise time using one of the equations shown throughout the text:

To use this equation, remember that, at the point of maximum height, the projectile's final velocity is zero. As informed by the exercise, the projectile's launch velocity is 20 m/s. Thus:

b) Knowing the time required for the projectile to reach its maximum height, we can easily calculate this height. For this, we will use the following list:

In the above calculation, we take into account that the projectile was launched from the ground, so y0 = 0.
c) We can easily calculate the projectile's velocity for the instants t = 1.0 s and t = 3.0 s using the hourly velocity function. Watch:

After the calculations, we find the values of 10 m/s and -10 m/s for the instants of time t = 1.0 s and t = 3.0 s, respectively. This indicates that, at the time of 3.0 s, the projectile is at the same height as at the time of 1.0 s. However, the movement occurs in the opposite direction, since the rise time of this projectile is 2.0 s. After this time interval has elapsed, the projectile begins its free-fall movement.
By Me. Rafael Helerbrock