We are always looking for applications for mathematics in practical activities or in the study of other sciences. There are mathematical contents that are completely abstract, not used in everyday life, but a large part of this science has practical application, helping in activities of more or less complexity. Physics is one of the sciences that makes the most use of mathematics to explain natural phenomena. We can observe processes of similarity of figures in optical studies, equations in the second degree in the calculation of centripetal force, use of the 1st degree function in kinematics, among other examples.
We will see one more application of the 1st degree function in physics, more precisely in the study of elastic force.
Think of a spring with one end fixed to a support, in a state of rest, that is, without suffering the action of any force. When applying a force F at the other end, the spring undergoes a deformation (stretch or compress) depending on the direction in which the force was applied. Robert Hooke (1635 – 1703), studying the deformations of springs, observed that they increase in proportion to the strength of the force.

In light of his observations, he established Hooke's law:
F = kx
Where,
F → is the force applied in newtons (N)
k → is the elastic constant of the spring (N/m)
x → is the deformation suffered by the spring (m)
Note that Hooke's law is a function that depends exclusively on the deformation of the spring, since k is a constant value (elastic constant). It could be written as follows:
F(x) = kx → a 1st degree function or affine function.
Example 1. A 7.5 kg block, in balance, is attached to one end of a spring, whose elastic constant is 150N/m. Determine the deformation suffered by the spring, considering g = 10m/s2.
Solution: As the system is in equilibrium, we can say that the resultant of the forces is equal to zero, that is:
F - P = 0 or F = P =mg
We know that m = 7.5 kg.
Thus,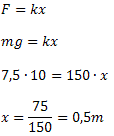
Example 2. A spring has one of its ends fixed to a support. When applying a force at the other end, the spring undergoes a deformation of 3m. Knowing that the spring constant is 112 N/m, determine the strength of the applied force.
Solution: We know, according to Hooke's law, that the deformation of the spring is proportional to the strength of the force. So, we have to:
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
1st degree function -Roles - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/funcao-1-o-grau-forca-elastica.htm

