You points of maximum it's from Minimum are defined and discussed only for high school functions, since they can exist on any curve.
Before, let's remember: a occupation of seconddegree is one that can be written in the form f (x) = ax2 + bx + c. O graphic of this type of function is the parable, who can have your concavity face down or up. Also, in this figure, there is a point called vertex, represented by the letter V, which is can be the Scoreinmaximum or the ScoreinMinimum of the function.
maximum point
All occupation of seconddegree with < 0 has Scoreinmaximum. In other words, the maximum point is only possible in functions with the concavity facing down. As shown in the following image, the maximum point V is the highest point of the second degree functions with a < 0.

Note that the graphic of this occupation is increasing until reaching the Scoreinmaximum, after that, the graph becomes descending. The highest point of this example function is its maximum point. Also note that there is no point with a y coordinate greater than V = (3, 6) and that the x value assigned to the maximum point is at the midpoint of the
segment, whose ends are the roots of function (when they are real numbers).Also, remember that the Scoreinmaximum always coincides with the vertex of the function with concavity facing downwards.
Minimum point
All occupation of seconddegree with coefficient a > 0 has ScoreinMinimum. In other words, the minimum point is only possible in functions with concavity facing upwards. Note in the following figure that V is the lowest point of the parabola:
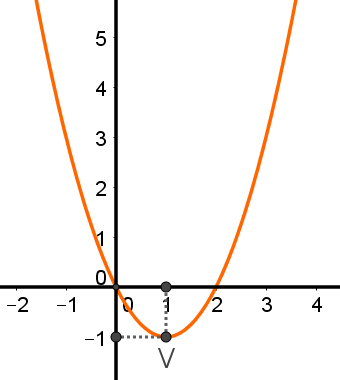
The graph of this occupation is decreasing until reaching the ScoreinMinimum, after that, continues growing. In addition, the minimum point V is the lowest point of this function, that is, there is no other point with a y coordinate lower than –1. Also note that the value of x related to y at the minimum point is also at the midpoint of the segment, whose endpoints are the roots of the function (when they are real numbers).
Also remember that the ScoreinMinimum always coincides with the vertex of the function with concavity facing upwards.
Maximum or minimum point in the function formation law
Knowing that the law of formation of occupationofseconddegree has the form f (x) = ax2 + bx + c, it is possible to use relations between the coefficients a, b and c to find the coordinates of the vertex of the function. The coordinates of the vertex will be exactly the coordinates of its point of maximum or of Minimum.
Knowing that the x coordinate of the vertex of a occupation is represented by xv, we will have:
Do not stop now... There's more after the advertising ;)
xv = - B
2nd
Knowing that the y coordinate of the vertex of a occupation is represented by yv, we will have:
yv = – Δ
4th
Therefore, the coordinates of the vertex V will be: V = (xvyv).
If the vertex will be point of maximum or of Minimum, just analyze the concavity of the parable:
If a < 0, the parabola has peak point.
If a > 0, the parabola has minimum point.
Note that when the function has two real roots, xv will be at the midpoint of the segment, whose ends are the roots of the occupation. So another technique to find xv and yv is to find the roots of the function, find the midpoint of the straight line connecting them, and apply that value to the function to find yv related.
Example:
Determine the vertex of the function f(x) = x2 + 2x – 3 and say if it is Scoreinmaximum or of Minimum.
1st Solution: Calculate the coordinates of the vertex by the given formulas, knowing that a = 1, b = 2 and c = – 3.
xv = - B
2nd
xv = – 2
2·1
xv = – 1
yv = – Δ
4th
yv = – (22 – 4·1·[– 3])
4·1
yv = – (4 + 12)
4
yv = – 16
4
yv = – 4
So, V = (– 1, – 4) and the function has ScoreinMinimum, because a = 1 > 0.
2nd Solution: Find the roots of occupation of seconddegree, determine the midpoint of the connecting segment, which will be xv, and apply that value to the function to find yv.
The roots of the function, given by the square completion method, they are:
f(x) = x2 + 2x – 3
0 = x2 + 2x – 3
4 = x2 + 2x – 3 + 4
x2 + 2x + 1 = 4
(x + 1)2 = 4
Doing the square root on both members, we will have:
√[(x + 1)2] = √4
x + 1 = ± 2
x = ± 2 - 1
x’ = 2 - 1 = 1
x" = – 2 – 1 = – 3
A segment that goes from – 3 to 1 has as its midpoint xv = – 1. For more details, check the image after the solution. Applying xv in the function, we will have:
f(x) = x2 + 2x – 3
yv = (– 1)2 + 2(– 1) – 3
yv = 1 – 2 – 3
yv = 1 – 5
yv = – 4
These results are the same values found in the first solution: V = (– 1, – 4). In addition, the function has ScoreinMinimum, because a = 1 > 0.
The image below shows the graph of this occupation with its roots and with its minimum V point.
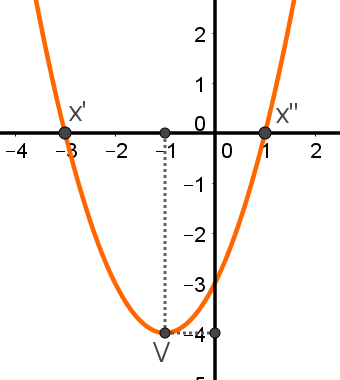
It is worth noting that Bhaskara's formula can also be used to find the roots of the function in this content.
By Luiz Paulo Moreira
Graduated in Mathematics