We say that a body moves in an oscillatory way when it performs movements (back and forth) around a certain position that is in balance.
Oscillatory movement is also known as periodic movement, because it depends on a period, which is the time needed to complete an oscillation.
The period of an oscillation in turn is mathematically represented by the equation:

Where:
T = period
f = frequency
1 = time needed to complete an oscillation
Any movement that happens at regular time intervals is called periodic movement or harmonic movement.
The simplest example of an oscillatory movement that exists is the simple pendulum movement. We can consider the pendulum clock as the classic example of this type of movement.
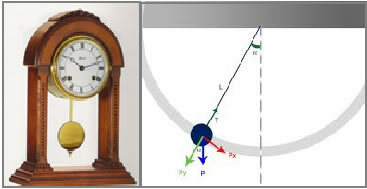
On the left is a grandfather clock. On the right, the oscillatory movement performed by him.
The displacement performed by the clock's pendulum is a mathematical equation:

xm, cos and φ are constants.
Where:
xm = amplitude
Positive constant that depends on how the movement is performed.
(ωt + φ) = movement phase
ω= angular frequency
φ = phase constant
This equation indicates periodic motion and is a sinusoidal function of time.
By Talita A. angels
Graduated in Physics
Brazil School Team
waves - Physics - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/fisica/movimento-oscilatorio.htm
