We say that Derivative is the rate of change of a function y = f(x) with respect to x, given by the relation ∆x / ∆y. Considering a function y = f (x), its derivative at the point x = x0 corresponds to the tangent of the angle formed by the intersection between the line and the curve of the function y = f (x), that is, the slope of the line tangent to curve.
According to the relationship ∆x / ∆y, We have to: 
starting from the idea of the existence of the limit. We have the instantaneous rate of change of a function y = f(x) with respect to x is given by the expression dy / dx.
We need to be aware that Derivative is a local property of the function, that is, for a given value of x. That's why we can't involve the entire function. Look at the graph below, it demonstrates the intersection between a line and a parabola, 1st degree function and 2nd degree function respectively:
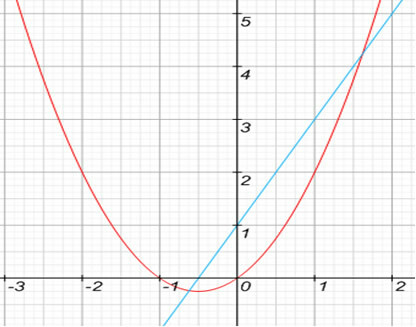
The straight line consists of the derivation of the function of the parabola.
Let's determine the variations of x when it increases or decreases its values. Assuming that e x varies from x = 3 to x = 2, find ∆x and ∆y.
∆x = 2 – 3 = –1
Now let's determine the derivative of the function. y = x² + 4x + 4.
y + ∆y = (x + ∆x) ² + 4 (x + ∆x) + 4 – (x² + 4x + 4)
= x² + 2x∆x + ∆x² + 4x + 4∆x + 4 - x² - 4x - 4
= 2x∆x + ∆x² + 4∆x
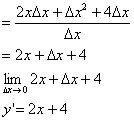
The derivative of the function y = x² + 4x + 8 is the function y’ = 2x + 4. Look at the graphic:
by Mark Noah
Graduated in Mathematics
Brazil School Team
Occupation - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/introducao-ao-estudo-das-derivadas.htm