One parable is the geometric representation of a high school function, which in turn is any function that can be written in the form f (x) = ax2 + bx + c. In this function, the letters a, b and c represent real numbers constants, called coefficients. The letter x, on the other hand, is called a variable, as it can take any value within the domain of this occupation. The coefficient "a" of these functions determines the concavity gives parable that represents them.
concavity of the parable
If the occupationofseconddegree can be written in the form f (x) = ax2 + bx + c, so it can be represented by a parable which, necessarily, will meet one of the following two conditions:
If a > 0, a concavity of the parable is turned upwards.
If a < 0, a concavity of the parable is turned down.
Therefore, coefficient "a" of a occupationofseconddegree determines where the concavity of this figure will be facing.
What is concavity?
THE concavity of a parable is a recess in this figure and is indicated, as we have seen, by the value of the coefficient “a”. To better understand this issue and what concavity is, observe the following two cases, the discussions that involve them and the images linked to them:
Case 1: Concavity facing down
when the concavity of a parable is facing down, this figure has a point, called a vertex, that has the largest possible y-coordinate. In the graph, there is no point that belongs to a parabola with a concavity facing downwards above the vertex. On the other hand, given any point P belonging to this parabola, there will always be another point T with y coordinate smaller than the y coordinate of point P.
The following image shows a parable with the concavity face down. These parables represent functions whose coefficient a is less than zero.

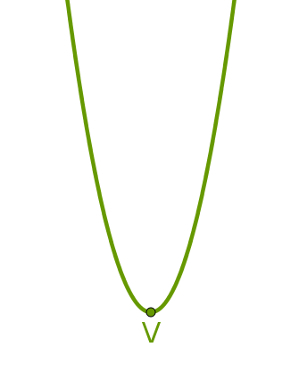
Case 2: Concavity facing up
when the parable It has concavity facing upwards, it is possible to find in it a point, called vertex, which, among all the points of the parabola, is the lowest. In other words, any other point in this parabola will have, as the y-coordinate, a number greater than the y-coordinate of the vertex. So the y of the vertex is the smallest possible y coordinate for this kind of parabola.
The following image shows a parable with the concavity facing up and its apex. This parabola represents a function of the second degree whose coefficient a is greater than zero.
by Luiz Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-concavidade-uma-parabola.htm
